WLB-LLM：用于大语言模型训练的工作负载均衡4D 并行方案

介绍

本文是WLB-LLM: Workload-Balanced 4D Parallelism for Large Language Model Training的译文整理。

Notes

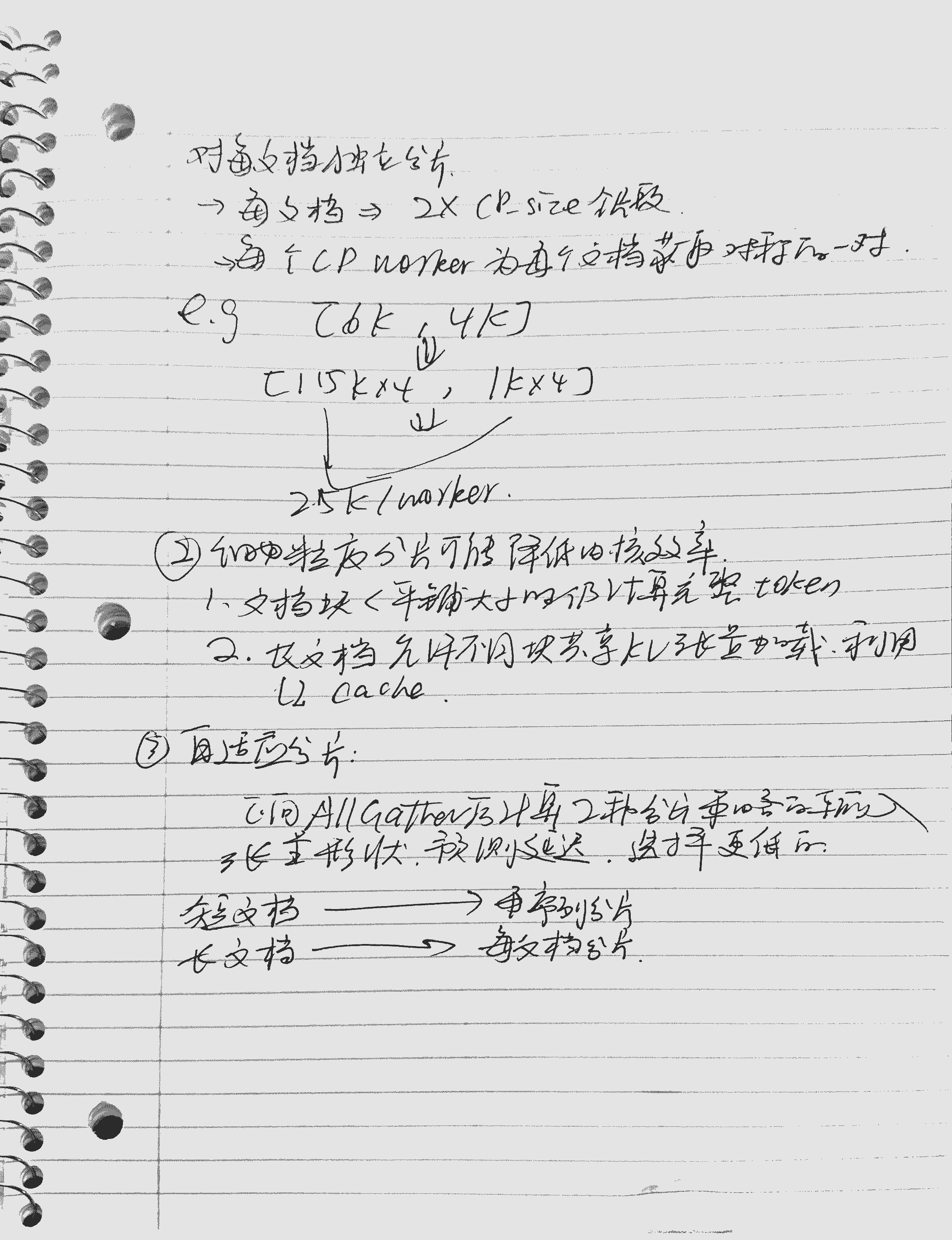
摘要

在这项工作中，我们提出了 WLB-LLM，一种用于大语言模型训练的 工作负载均衡 4D 并行机制。我们首先对 LLM 训练中的工作负载不均衡问题进行了全面分析，并识别出不均衡主要来源于 流水线并行 和 上下文并行 两个层面。随后，为了解决这一问题，在流水线并行层面，WLB-LLM 引入了一种 面向工作负载感知的可变长度文档打包方法，以在不同 micro-batch 之间平衡计算与通信负载。此外，在上下文并行层面，WLB-LLM 提出了一种新的 细粒度逐文档分片策略，确保同一上下文并行组内的每个工作节点具有完全一致的工作负载。在不同模型规模下的综合实验表明，WLB-LLM 能够显著缓解 4D 并行 LLM 训练中的工作负载不均衡问题，并在我们的内部 LLM 训练框架中实现了 平均 1.23× 的加速比。

引言

大语言模型（LLMs）已被广泛应用为多种应用的核心支撑，例如 代码助手、语言翻译 以及 聊天机器人。LLM 所展现出的卓越能力和广阔前景，引发了大型科技公司之间训练更高智能、更强通用性模型的激烈竞争。随着 LLM 的模型规模以及上下文窗口长度持续增长，LLM 的训练过程消耗了大量的计算资源。例如，Meta 报告称，LLaMA3-405B 模型的训练使用了 16K 张 H100 GPU，持续数月之久。如此巨大的计算成本使得端到端训练效率的任何改进都能够转化为可观的资源节省。

然而，在大规模 LLM 训练任务中，由于 工作负载不均衡 问题，大量 GPU 资源未能得到充分利用。为说明这一现象，图 1(a) 展示了在一个上下文窗口长度为 128K、跨 8K 张 H100 GPU 执行的 405B LLM 训练任务中，各 GPU 的归一化计算时延情况。可以观察到，不同 GPU 之间的计算时延存在显著差异，其中最慢的 GPU 其计算时延比其他 GPU 高出 1.44×。由于训练过程具有同步特性，这种计算时延差异会导致所有其他 GPU 必须等待最慢的 GPU 完成计算，从而显著降低整体训练效率。

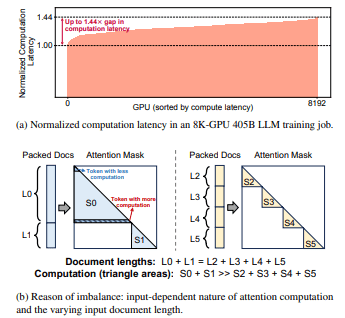图 1： 大规模 LLM 训练任务中观察到的工作负载不均衡问题及其成因。

工作负载不均衡的根本原因在于 注意力计算对输入的依赖性 以及训练数据中 输入文档长度的差异性。如 图 1(b) 所示，输入序列通常由多个输入文档组成。为了在长上下文训练中保证模型质量，会使用 注意力掩码 来阻止同一序列中不同文档之间的 token 互相关注。这种做法引入了 逐 token 算术强度的异构性，因为位于长文档尾部位置的 token 需要执行更多的注意力计算。因此，即使总序列长度相同，包含长文档的输入序列也会产生显著更高的计算负载。

然而，现有的 LLM 训练框架未能识别 逐 token 算术强度的异构性。具体而言，最先进的 LLM 训练方案采用了一种 4D 并行范式，将 数据并行（DP）、流水线并行（PP）、上下文并行（CP）以及 张量并行（TP）相结合。输入文档在 DP 和 PP 层面被打包为 固定长度 的序列，随后在 CP 和 TP 层面被切分并分发为多个 chunk。这种 固定且静态 的训练流程将所有输入 token 视为同质，并为每个 GPU 分配相同数量的 token，不可避免地导致 GPU 之间的工作负载不均衡。此外，随着模型规模增大以及上下文窗口变长，这一问题被进一步放大，极长文档更容易出现在输入 batch 中，从而拖慢整个训练步骤。

一种直观的解决思路是通过 打乱并重新打包输入文档，以在不同 micro-batch 之间更均匀地分配计算负载。然而，该方法在实践中并不有效，主要原因有两点： 首先，要通过打乱与重打包实现有效平衡，需要一个跨越多个 全局 batch 的足够大的打包窗口。这会影响数据采样与加载的随机性，从而可能对训练过程中的 模型收敛性 产生不利影响（如 §3.3 所讨论）。 其次，打乱与重打包只能缓解 micro-batch 之间 的工作负载不均衡，无法解决由于 序列切分 所导致的 文档内部不均衡。在 4D 并行训练中，输入序列会被划分为多个 chunk 并分配到不同 GPU。包含文档尾部的 chunk 需要其 token 关注更多前序 token，因此会产生更高的计算负载，从而在 GPU 之间造成 文档内部的工作负载不均衡。

为克服上述挑战并解决大规模 LLM 训练中严重的工作负载不均衡问题，我们提出了一种 灵活且输入感知的文档打包与分片方法，适用于 4D 并行训练范式。在该方法中，数据打包与分片不再生成具有固定 token 数量的 micro-batch；相反，每个 GPU 的目标是接收 总计算与通信负载相等 的输入 token。此外，为了尽量减小对数据随机性的影响，我们仅对 极长文档 的执行顺序进行调整。该设计基于我们的观察：长文档中的 token 仅占全部训练 token 的一小部分，但却对工作负载不均衡产生了最显著的影响。

基于上述设计洞见，我们构建了 WLB-LLM，一种用于大语言模型训练的 工作负载均衡 4D 并行机制。我们首先对 4D 并行下的 LLM 训练中的工作负载不均衡问题进行了系统分析（§3），并识别出跨不同并行层级的两个主要不均衡来源： （1）流水线并行层面 的 micro-batch 之间的不均衡； （2）上下文并行层面 的文档分片之间的不均衡。

针对这些不均衡问题，WLB-LLM 在不同并行层级分别提供了定制化的解决方案。在 PP 层面，WLB-LLM 引入了 可变长度文档打包，允许将多个短文档组合为更长的序列，从而使其总计算负载与单个长文档对齐（§4）。此外，WLB-LLM 通过 自适应延迟极长文档的执行，在保持较低逐 token 延迟的同时，实现了 micro-batch 之间近似最优的工作负载平衡，从而有效保留了数据加载的随机性。在 CP 层面，WLB-LLM 采用了一种新的 逐文档分片策略，确保同一 CP 组内的每个工作节点具有相等的工作负载（§5）。同时，我们观察到 逐文档分片 在内核效率与分片平衡性之间存在权衡。为最大化整体性能，我们提出了一种 启发式算法，能够在运行时根据输入序列自适应选择最优的分片策略。

本文的主要贡献如下：

• 据我们所知，这是首个在 4D 并行的大规模 LLM 训练 中系统识别、分析并解决 工作负载不均衡问题 的研究。
• 在 PP 层面，我们设计了 可变长度输入打包 与 自适应异常文档延迟策略，在最小化对数据加载随机性和模型收敛性影响的同时，实现了 micro-batch 之间的近最优工作负载平衡。
• 在 CP 层面，我们实现了一种 细粒度逐文档分片方法，并结合 自适应分片选择机制，在运行时为每个输入 micro-batch 选择最有效的分片策略。
• 我们进行了全面的实验评估，结果表明，WLB-LLM 在不同模型规模和上下文窗口长度下均实现了 平均 1.23× 的加速比。

背景

在本节中，我们介绍 4D 并行 LLM 训练 的背景，并讨论 长上下文 LLM 训练 中输入文档的特性。

4D 并行 LLM 训练

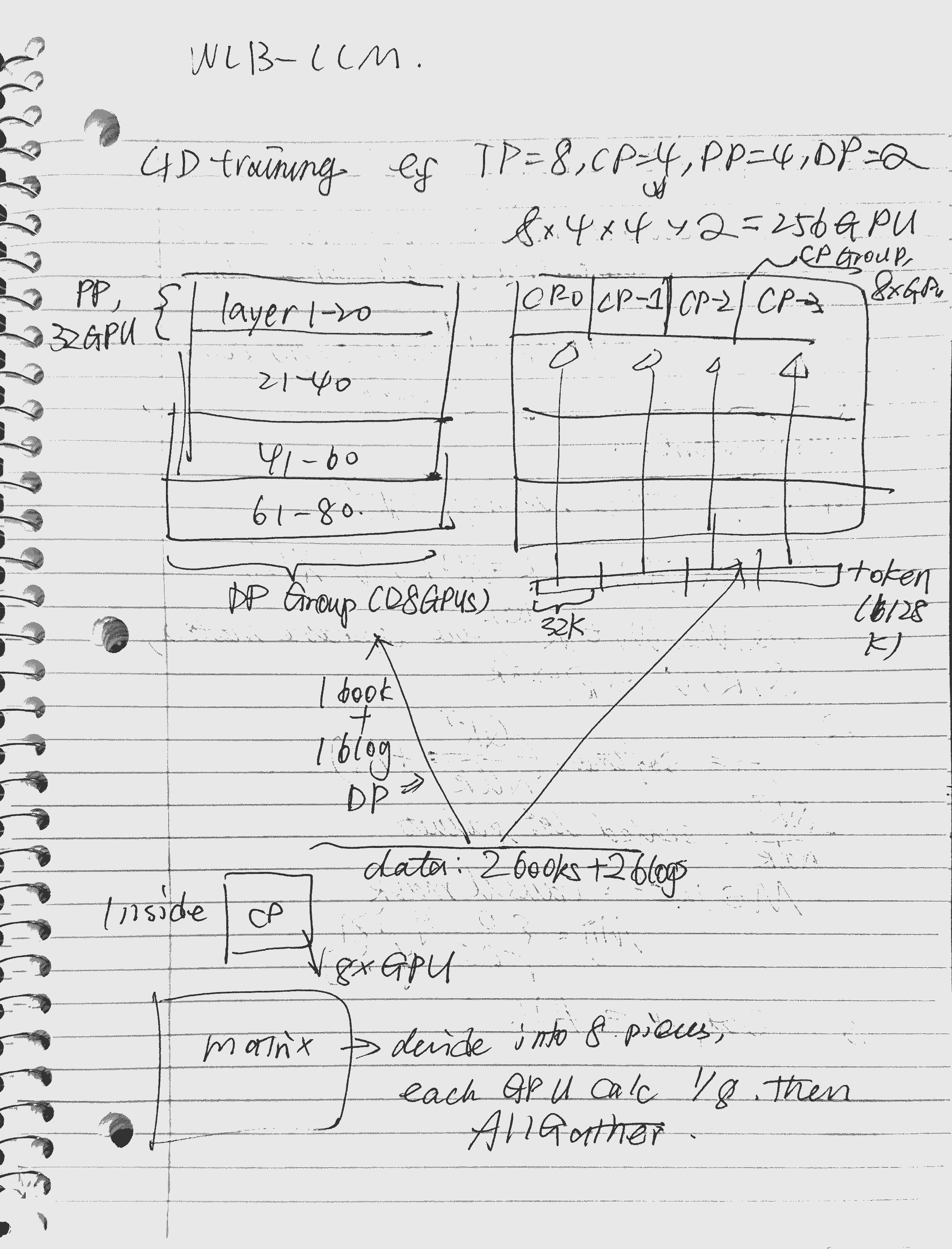
训练具有数十亿甚至数万亿参数的超大规模 LLM 极具挑战性，需要投入大量工程工作来调优 多层级并行机制。当前最先进的 LLM 训练框架采用 四维并行，包括 数据并行（DP）、流水线并行（PP）、上下文并行（CP）以及 张量并行（TP）。图 2 给出了一个 (TP=2, CP=2, PP=4, DP=4) 的 4D 并行示例。

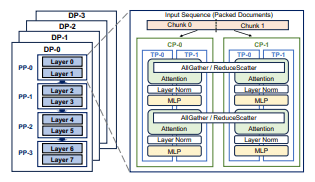图 2： 用于 LLM 训练的 4D 并行机制概览。

数据并行（Data Parallelism）：在 DP 中，输入的 全局 batch 被划分并分发到多个 DP 工作节点，每个节点持有全局 batch 的一部分。默认情况下，模型参数在各 DP 节点之间是 完全复制 的。一些先进技术（如 ZeRO 和 FSDP）会在 DP 节点之间划分模型参数、梯度以及优化器状态，以降低内存开销。在训练过程中，每个 DP 节点使用其本地 batch 独立计算参数更新，然后通过 AllReduce（或在使用 FSDP 时采用 ReduceScatter）与其他节点同步梯度。

流水线并行（Pipeline Parallelism）：在每个 DP 节点内部，设备会进一步通过流水线并行划分为多个 PP 工作节点。在 PP 中，模型按 层级方式 进行切分，每个 PP 节点负责若干层块。DP 节点的输入 batch 也会被拆分为多个 micro-batch。训练过程中，一个 micro-batch 会在前向传播中依次经过所有 PP 节点，在反向传播中再按相反方向返回。前向与反向阶段分别需要 点对点（P2P）通信 来传递激活值和梯度。

上下文并行（Context Parallelism）：CP 旨在解决 长上下文训练 中激活值占用内存过大的问题。如 图 2 所示，CP 会复制模型参数，但沿着 序列长度维度 对输入和激活进行分片，并分布到不同的 CP 工作节点。CP 可以采用基于 环形 P2P 通信 的方式运行，或在前向阶段使用 AllGather 来收集所有 token 的 KV（key 和 value）张量，并在反向阶段使用 ReduceScatter 来计算 KV 张量的梯度。其他算子（如 Linear 和 LayerNorm）则与 DP 类似，在各节点上独立执行。

张量并行（Tensor Parallelism）：TP 在 层内部（如注意力层、FFN）对模型参数进行切分，并分布到多个 TP 工作节点上。TP 通常与 序列并行（SP） 结合使用，以进一步切分输入张量和激活。在本文中，提到 TP 时默认同时包含 TP 和 SP。采用 TP 后，每个 GPU 仅持有部分输入和参数，因此在训练过程中需要频繁进行 AllGather 和 ReduceScatter 通信。基于这一原因，TP 通常应用于 单节点内部，而其他并行方式则跨节点使用。

输入文档长度的差异性

在大规模 LLM 训练中，输入文档的长度可能存在显著差异，尤其是在使用 大上下文窗口 的情况下。为说明这一点，我们对一个 128K 上下文长度 的训练任务中的数据特征进行了分析，如 图 3 所示。

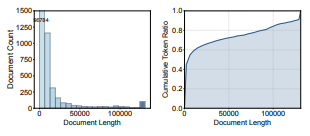图 3： 输入文档特性分析：输入文档长度分布（左）以及按文档长度统计的累计 token 比例（右）。

从 逐文档 的角度来看，输入文档长度分布呈现出高度 偏斜 的特性。如 图 3 左图 所示，大多数输入文档相对较短，但仍然存在少量 极长文档，其中最长的文档长度可达到完整的上下文窗口大小。只要一个极长文档出现在输入 batch 中，就很容易在 micro-batch 之间引发显著的工作负载不均衡。这一现象凸显了对 输入感知型解决方案 的需求，即通过考虑文档长度差异来动态平衡工作负载。

从 逐 token 的角度来看，我们统计了不同文档长度下的 累计 token 比例。如 图 3 右图 所示，大多数训练 token 来自相对较短的文档。例如，长度小于上下文窗口一半的文档贡献了 超过 75% 的训练 token。尽管长文档对工作负载平衡具有显著影响，但其所包含的 token 仅占整个训练数据集的一小部分。这一特性为 自适应延迟极长文档的执行 提供了机会，从而在缓解工作负载不均衡的同时，尽量减少对大多数 token 的数据采样随机性的影响。

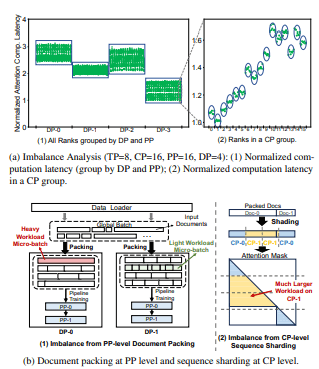图 4： 工作负载不均衡来源于 PP 层级的文档打包 以及 CP 层级的序列分片。

动机

为了阐明 WLB-LLM 的设计动机，我们首先对 4D 并行 LLM 训练 中不同并行层级的工作负载不均衡问题进行了深入分析。随后，我们介绍了一种 通过跨 batch 打乱并重新打包输入文档 的基线方案。最后，我们讨论了该基线方案为何无法完全消除工作负载不均衡，并分析了 输入打包均衡性 与 模型收敛性 之间的权衡关系。

不均衡分析

在分析了我们内部一个 8K GPU、128K 上下文窗口、405B LLM 训练任务的性能追踪结果后，我们识别出两种主要的工作负载不均衡来源：（1）PP 层级 micro-batch 之间的不均衡；（2）CP 层级序列分片之间的不均衡。为说明这一点，我们统计了每个 GPU 上的 注意力计算时延，结果如 图 4 所示。

PP 层级不均衡

如 图 4(a)(1) 所示，不同 DP 工作节点之间的注意力计算时延存在显著差异。在每个 DP 工作节点内部，可以观察到由数据点形成的“竖直线”，其中每个点代表该 DP 节点内的一个 PP 工作节点。由于同一 DP 节点内的 PP 工作节点处理的是 相同的一组 micro-batch，因此它们的工作负载几乎一致。

基于 图 4(a)(1) 的结果，我们可以得出结论：DP 和 PP 层级的工作负载不均衡均源于 micro-batch 之间的不均衡，而这种不均衡是由 输入打包过程 引起的。如 图 4(b) 左图 所示，输入文档被打包为 等长度 的序列（micro-batch）。尽管这种固定长度打包策略保证了每个 PP 和 DP 工作节点处理相同数量的 token，但 逐 token 计算强度的差异 会导致工作负载不均衡。例如，仅包含一个长文档的 micro-batch（红色标注）相比由多个短文档组成的 micro-batch（绿色标注）具有更大的计算负载。

CP 层级不均衡

为了更清晰地展示 CP 层级的不均衡现象，我们放大观察了某一个特定的 PP 工作节点（也称为一个 CP 组）。如 图 4(a)(2) 所示，不同 CP 工作节点之间（以圆圈标示）存在显著的工作负载不均衡，而同一 CP 工作节点内部的 TP 工作节点计算时延则基本一致（圆圈内的数据点）。

这种 CP 工作节点之间的不均衡源于 CP 层级的序列分片方式。如 图 4(b)(2) 所示，输入序列被划分为 包含相同 token 数量 的多个 chunk，并分配给不同的 CP 工作节点。当前最先进的方法会将输入序列划分为 2 × CP_size 个 chunk，并将第 i 个 CP 工作节点分配第 i 个以及第 (2 × CP_size − 1 − i) 个 chunk，以实现更好的负载均衡。当序列仅包含单个文档时，这种分片策略效果良好；然而，当序列由多个文档打包而成时，便可能在 CP 工作节点之间引入显著的不均衡，如图所示。

尽管序列 chunk 会进一步在 TP 层级进行切分和分发，但在 TP 层级并未观察到不均衡。这是因为在计算之前，所有 TP 工作节点都会执行一次 AllGather 操作来收集完整的序列 chunk。因此，同一 CP 工作节点内的所有 TP 工作节点处理的是 相同的序列 chunk，从而消除了 TP 层级的不均衡。

不均衡传播

在训练过程中，工作负载不均衡会从 内层并行机制 向 外层并行机制 逐级传播，并不断累积和放大，最终对 端到端训练时延 产生显著影响。在 DP、CP 和 TP 中，训练过程中会执行 AllReduce、AllGather 和 ReduceScatter 等 集合通信 操作，所有工作节点都以同步方式运行。因此，一个 DP、CP 或 TP 组的训练时延由该组中 最慢的工作节点 决定。

相比之下，PP 层级中不同的 PP 工作节点之间存在 生产者–消费者 的关系。如 图 5 所示，PP 的关键路径由 最大 micro-batch 在所有 PP 工作节点上的处理时延，以及 其余 micro-batch 在第一个 PP 工作节点上的前向与反向传播时延 共同决定。PP 工作节点之间这种独特的数据依赖关系会进一步放大不均衡，对总训练时延产生更大的影响。

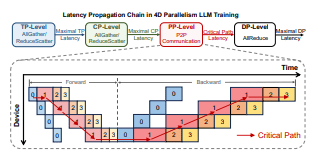图 5： 4D 并行 LLM 训练中，不同并行层级之间的时延传播过程，PP 层级会放大工作负载不均衡的影响。

由于不均衡的逐级传播，micro-batch 训练时延的增加主要来自两个方面：（1）从内层并行机制传播而来的不均衡（如 CP 分片不均衡）；（2）由于 PP 层级打包导致 固有计算负载更大 的 micro-batch。这一现象表明，在所有并行层级中消除工作负载不均衡至关重要。

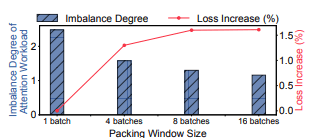图 6： 更大的打包窗口能够改善工作负载平衡，但会导致训练损失增加。

基线方案：固定长度打包

一种潜在的解决工作负载不均衡问题的方法是 优化输入文档的打包方式。当前的 4D 并行框架 要求所有 micro-batch 具有 统一的序列长度，该长度等于上下文窗口大小，以便实现高效的序列批处理。在这一固定长度约束之上，我们实现了一种 基线的打乱与打包优化方案，将输入文档打包为 等长度 的 micro-batch。

形式化地，给定来自一个或多个 全局 batch 的一组输入文档，其目标是将这些文档打包为若干个 总长度固定 的 micro-batch，并在所有 micro-batch 之间平衡 注意力计算工作负载。在不失一般性的情况下，我们以 因果掩码 为例来计算注意力工作负载。对于因果掩码，一个 micro-batch 的注意力计算工作负载与下式成正比：

$$ \sum_{i=1}^{N} d_i^2 $$

其中，$d_i$ 表示该 micro-batch 中第 $i$ 个文档的长度。

搜索最优文档打包方案是一个 NP-hard 问题，因为该问题可以由经典的 数划分问题 扩展而来，同时引入了 求和约束 以及 平方和目标函数。为寻找最优打包方案，我们将该任务表述为一个 整数线性规划（ILP） 问题。假设共有 $N$ 个文档，每个文档长度为 $d_i$，需要将其打包为 $M$ 个 micro-batch，每个 micro-batch 的总长度为 $S$。目标是最小化 micro-batch 中的最大工作负载：

$$ \begin{aligned} \min ;& \max_{j=1,\ldots,M} \sum_{i=1}^{N} x_{ij} d_i^{2} \ \text{s.t.};& \sum_{j=1}^{M} x_{ij} = 1, \quad i = 1, \ldots, N \ & \sum_{i=1}^{N} x_{ij} d_i \le S, \quad j = 1, \ldots, M \ & x_{ij} \in {0,1} \end{aligned} $$

其中，$x_{ij}$ 是一个 二值变量，表示文档 $i$ 是否被打包到第 $j$ 个 micro-batch 中。具体而言，$x_{ij}=1$ 表示文档 $i$ 被分配到 micro-batch $j$。基于该 ILP 表述，我们使用 商用求解器 来获得最优打包方案。

权衡分析

在更多 全局 batch 范围内优化输入文档打包，有助于实现更高程度的工作负载平衡。然而，这也会调整更多输入文档的 执行顺序，从而影响数据采样与加载的 随机性。这种影响可能会降低模型质量，并对 模型收敛性 产生负面影响。

为评估 打包平衡性 与 模型质量 之间的权衡关系，我们对一个 5.5 亿参数 的模型进行了 52K 步 预训练，并使用了不同大小的 打包窗口。随后，我们评估了在不同设置下，输入 batch 在打包后的 工作负载不均衡程度。不均衡程度定义为：

$$ \frac{\text{Max_Attn}}{\text{Avg_Attn}} $$

其中，Max_Attn 表示全局 batch 中 最大的注意力计算工作负载，Avg_Attn 表示该全局 batch 内所有 micro-batch 的 平均注意力计算工作负载。

如 图 6 所示，当仅在单个全局 batch 内进行打包优化时，micro-batch 之间的工作负载不均衡仍然较为严重。随着参与打包优化的全局 batch 数量增加，固定长度打包可以实现更好的工作负载平衡。然而，由于 对更多输入文档进行重新打包 会降低数据加载的随机性，最终的训练损失随之上升。这些结果表明，朴素的固定长度打包优化无法在不牺牲模型质量的前提下实现理想的工作负载平衡，从而凸显了对更先进解决方案的需求。

打包平衡性 与 模型质量 之间的权衡促使我们打破 micro-batch 的固定长度约束，并设计一种 更加灵活的打包策略。在接下来的两个章节中，我们将详细介绍 WLB-LLM 的设计，包括 PP 层级的可变长度打包与启发式异常文档延迟优化，以及 CP 层级的细粒度与自适应分片优化。

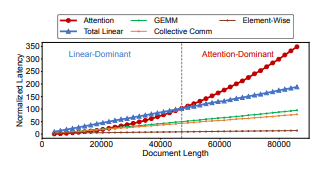图 7： 操作时延与输入文档长度之间的关系（其中 Total Linear 表示 GEMM、集合通信 以及 逐元素算子 的总和）。

用于 PP 的可变长度打包与异常文档延迟

在 PP 层级，我们专注于通过 以工作负载感知的方式重新打包输入文档，来平衡不同 micro-batch 之间的工作负载。首先，我们设计了一种 可变长度打包策略，在相同打包窗口大小下，相比固定长度打包能够实现更高程度的工作负载平衡（§4.1）。其次，我们提出了一种 异常文档延迟方法，用于自适应地延迟训练 极长文档。该方法在实现 micro-batch 之间近似最优工作负载平衡的同时，尽量减小对数据随机性的影响（§4.2）。最后，我们设计并实现了一种 高效的启发式算法，能够在运行时以 可忽略的开销 完成打包优化（§4.3）。

工作负载感知的可变长度打包

基线方案中 固定长度打包 的主要局限在于：当全局 batch 中存在一个极长文档时，无法实现工作负载平衡。例如，如果某个文档的长度等于上下文窗口大小，由于注意力计算具有 平方级复杂度，就不可能再构造一个仅由短文档组成、但计算负载相同的 micro-batch。

为解决这一问题，我们提出了一种 可变长度打包策略，允许每个 micro-batch 具有 不同的序列长度。该设计的关键洞见在于：一个 micro-batch 的工作负载并不仅由 注意力计算 决定。GEMM 计算、逐元素算子 以及 集合通信（如 AllGather 和 ReduceScatter）同样对训练时延有重要贡献，并且也会受到 micro-batch 中文档长度的影响。

为说明这一点，我们在 图 7 中展示了 操作时延 与 文档长度 之间的关系。该结果来自一个在 16 张 H100 GPU 上训练 LLaMA2 7B 模型的任务，所有时延均归一化为 文档长度为 4096 时的注意力计算时延。可以观察到，注意力计算时延 随输入文档长度呈 二次增长，而其他操作（如 GEMM、集合通信 和 逐元素算子）的时延则与文档长度呈 线性关系。

这一特性为进一步提升超越固定长度打包的工作负载平衡性提供了机会。如果一个长文档的 注意力计算时延 显著高于其他操作，我们可以将多个短文档打包在一起，以延长 其他操作 的执行时延，从而使其 总时延 与长文档相匹配。

基于这一思想，我们将固定长度打包扩展为 可变长度打包。优化目标从仅平衡注意力计算负载，转变为平衡 包括所有操作在内的总工作负载：

$$ \begin{aligned} \min \quad & \max_{j=1,\ldots,M} \sum_{i=1}^{N} \Big( W_a(x_{ij} d_i)

• W_l(x_{ij} d_i) \Big) \ \text{s.t.}\quad & \sum_{j=1}^{M} x_{ij} = 1, \quad i = 1, \ldots, N \ & \sum_{i=1}^{N} x_{ij} d_i \le S_{\max}, \quad j = 1, \ldots, M \ & x_{ij} \in {0,1} \end{aligned} $$

其中，$W_a(\cdot)$ 和 $W_l(\cdot)$ 分别表示 注意力计算时延 与 其他所有操作的时延 的预测函数，二者均可通过 离线性能剖析 得到；$S_{\text{max}}$ 表示由 GPU 内存约束 所允许的最大序列长度。

异常文档延迟

可变长度打包策略通过允许将多个短文档打包为 超过固定上下文窗口大小 的长序列，从而实现了更高程度的负载平衡。然而，在单个全局 batch 内，短序列的数量 可能仍不足以在所有 micro-batch 之间完全平衡计算工作负载。

为解决这一问题，我们提出了 自适应延迟异常文档执行 的方法，即对 极长文档 进行延迟处理。该方法基于我们的一个关键观察：尽管这些异常文档对工作负载不均衡具有显著影响，但它们在训练中仅贡献了 极少比例的 token（如 §2.2 所述）。通过有选择地延迟少量极长文档中 token 的训练，我们可以在 最大程度平衡 micro-batch 工作负载 的同时，最小化对数据随机性的影响。

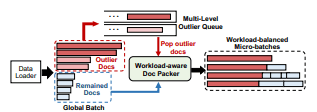图 8： 可变长度打包与异常文档延迟相结合的处理流程。

整体流程

如 图 8 所示，我们为 异常文档 实现了一个 多级等待队列。假设共有 $n$ 个异常队列，每个队列对应一个超参数 $L_i$，用于指定第 $i$ 个队列中 文档长度的最小阈值，其中 $L_1 < L_2 < \cdots < L_{n+1}$。

当一个新的 全局 batch 到达时，长度大于 $L_1$ 的文档将被视为异常文档，并被加入对应的等待队列 $i$，满足 $$ L_i \le d < L_{i+1} $$ 其中 $d$ 表示文档长度。异常队列中的文档执行将被延迟，直到队列中累计了足够数量的异常文档。一旦某个队列的大小达到 一个全局 batch 中 micro-batch 的数量，这些异常文档就会从队列中弹出，并分别加入到每一个 micro-batch 中。这样可以保证 micro-batch 之间的工作负载均衡，因为每个 micro-batch 都会获得 数量相同的异常文档。

超参数 $L_i$ 的调节

超参数 $L_i$ 的选择会直接影响系统性能。相邻两个超参数 $L_i$ 与 $L_{i+1}$ 之间的 间隔越小，同一队列中的文档长度差异就越小，从而能够实现 更高程度的工作负载平衡。然而，较小的间隔也意味着队列中需要 更长时间 才能积累足够的文档进行联合处理，从而增加 逐 token 的延迟。

为了选择合适的 $L_i$ 值，我们从训练数据中 采样一小部分文档，并在该子集上运行打包算法（§4.3 中介绍），同时评估 micro-batch 之间实现的工作负载平衡程度 以及 由此产生的逐 token 延迟。最终，我们选择在保持较低逐 token 延迟的前提下，能够最大化工作负载平衡的 $L_i$ 取值。

启发式打包算法

尽管可以通过 ILP 求解器 为给定的一组输入文档推导出最优打包方案，但其求解时间在运行时开销过高，难以实际应用。同时，离线优化文档打包也不可行，因为需要为不同训练配置存储大量 预打包数据集，会引入显著的存储开销。

为此，我们设计了一种 启发式算法，将 可变长度打包 与 异常文档延迟优化 相结合，在运行时高效生成 工作负载均衡的 micro-batch。如 算法 1 所示，该算法以数据加载器 $D$、采用 FIFO 方式运行的异常文档多级等待队列 $Q$、每次迭代的 micro-batch 数量 $N$，以及序列长度上界 $S_{\text{max}}$ 作为输入。算法的输出是在每次训练迭代中生成的一系列 负载均衡的打包输入 batch。

打包过程首先遍历数据加载器 $D$ 中的输入 batch，并将所有异常文档加入 $Q$ 中对应的等待队列以进行延迟处理（第 4–10 行）。如果 $Q$ 中任意一个队列 $q$ 的大小达到 $N$，则将 $q$ 中的文档弹出，并加入当前 batch 的 待处理文档集合（第 11–15 行）。随后，算法采用 贪心方式 进行打包：先处理剩余文档，再处理新加入的长文档。对于每个文档，算法首先尝试将其打包到 当前工作负载最小 的 micro-batch 中（工作负载通过式 (2) 中定义的 $W_a(\cdot)$ 和 $W_l(\cdot)$ 计算），前提是该 micro-batch 的总长度不超过 $S_{\text{max}}$。如果该尝试不可行，则转而将文档打包到 当前长度最小 的 micro-batch 中（第 20–27 行）。无法满足上述约束的文档将被保留到下一次迭代中处理（第 29 行）。

该启发式方法能够有效地将 异常文档延迟 与 可变长度打包 结合起来，在运行时高效地平衡所有 micro-batch 之间的计算工作负载。

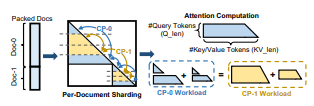图 9： 细粒度逐文档分片机制概览。

用于 CP 的细粒度与自适应分片

在 CP 层级，我们通过实现一种 细粒度逐文档分片策略 来提升文档分片之间的工作负载均衡，确保每个 CP 工作节点获得 相等的计算负载（§5.1）。此外，我们观察到 注意力内核效率 与 分片粒度 之间存在权衡关系（§5.2）。为最大化整体性能，我们进行了深入分析，并针对给定输入序列 自适应地选择最优分片策略（§5.3）。

逐文档分片设计

在 CP 层级，micro-batch 的序列会被分片并分配到不同的 CP 工作节点上，每个 CP 工作节点负责一个 独占的序列分片。现有的 CP 实现采用的是 逐序列分片（Per-Sequence Sharding） 策略，将整个输入序列均匀划分为 2 × CP_size 个 chunk。当输入序列由多个文档打包而成时，该方法很容易导致 注意力计算工作负载的显著不均衡。

为消除 CP 层级的工作负载不均衡问题，我们提出了一种 细粒度分片方案。具体而言，我们采用 逐文档分片（Per-Document Sharding），将 每个文档 划分为 2 × CP_size 个文档 chunk。如 图 9 所示，每个 CP 工作节点会从 每个输入文档 中获得一对 对称的 chunk。通过这种细粒度逐文档分片策略，每个 CP 工作节点不仅获得 相同数量的 token（从而保证 GEMM 计算 与 集合通信 的负载均衡），同时也获得 相同的注意力计算工作负载。

避免填充

细粒度逐文档分片将每个输入文档划分为 2 × CP_size 个文档 chunk。然而，文档长度并不总是能被 2 × CP_size 整除，这通常需要通过 填充 token 来扩展文档长度，从而引入冗余计算。为避免由文档填充带来的额外开销，我们设计了一种 无填充的逐文档分片方法。

具体而言，我们将每个文档拆分为两部分：一部分长度可被 2 × CP_size 整除，另一部分为剩余 token。假设第 $i$ 个文档的长度为 $d_i$，满足 $$ d_i = e_i + r_i $$ 其中 $$ e_i = \left\lfloor \frac{d_i}{2 \times CP_size} \right\rfloor . $$

我们对 $e_i$ 部分应用标准的逐文档分片，而将 $r_i$ 中的 token 以 轮询（round-robin） 的方式分配给各个 CP 工作节点。由于 $\sum_{i=1}^{n} d_i$ 和 $\sum_{i=1}^{n} e_i$ 都能被 2 × CP_size 整除，因此 $$ \sum_{i=1}^{n} r_i = \sum_{i=1}^{n} (d_i - e_i) $$ 同样可以被 2 × CP_size 整除。这保证了每个 CP 工作节点获得 完全相同数量的 token，从而彻底消除了对填充的需求。

内核效率与分片均衡性的权衡

逐文档分片策略可以在 CP 层级 完全消除工作负载不均衡。然而，将每个文档拆分为多个更短的 chunk 可能会 降低内核效率。这种效率下降主要源于以下两个原因：

（1）Tile 级计算浪费：注意力计算会被划分为更小的 tile，并由不同的线程块在 GPU 上执行。例如，在 FlashAttention 的前向内核中，tile 大小被设置为 128。当 token 数量小于 tile 大小时，线程块仍然会对 128 个 token 执行完整计算，从而造成显著的计算浪费。为说明这一点，我们对 Query token 长度 在 16 到 256 之间变化时的注意力前向时延进行了剖析。如 图 10（左） 所示，当 Q_len 从 16 增加到 128 时，内核时延几乎保持不变，这是因为 所有长度小于 128 的短文档都会在内核层面被填充到 128 token。相比之下，当 Q_len 从 128 增加到 256 时，内核时延显著上升。

（2）张量内存加速器（TMA）利用效率不足：TMA 是 NVIDIA Hopper 架构引入的一项特性，支持 GPU 在 全局内存 与 共享内存 之间进行 异步拷贝。当文档长度较大（例如 Q_len ≥ 256）时，多个线程块可以在处理不同 Q token 的同时 共享同一文档 chunk 的 KV token。这使得 KV 张量加载可以通过 TMA 多播 借助 L2 缓存进行共享，从而显著降低从全局内存到共享内存的传输时延。如 图 10（右） 所示，当 Query 张量长度从 128 增加到 256 时，实现的 TFLOPs 显著提升，体现了 TMA 多播加载 的优势。

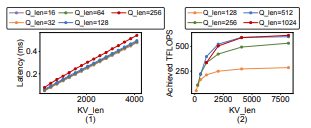图 10： 注意力内核性能剖析：（左）注意力前向计算时延；（右）注意力前向内核的实际 TFLOPs。

这些剖析结果清晰地表明了 注意力内核效率 与 CP 分片均衡性 之间的权衡关系。当对由短文档组成的输入序列应用逐文档分片时，可能会在内核层面引入冗余计算并降低实现的 TFLOPs，最终导致 注意力计算时延增加。

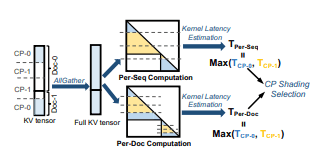图 11： 自适应 CP 分片策略选择流程。

自适应分片选择

基于 §5.2 的分析，尽管 细粒度逐文档分片 在 CP 层级实现了最优的工作负载均衡，但这并不一定保证性能最优，因为由逐文档分片生成的 更细粒度文档 chunk 可能会降低 注意力内核效率。为此，我们提出在 运行时 针对每个 micro-batch 自适应选择最优的分片策略。

如 图 11 所示，在 CP 层级的前向传播过程中，会在各个 CP 工作节点之间执行一次 AllGather 通信，以收集完整的 KV 张量。随后，我们分别计算 逐序列分片 与 逐文档分片 两种情况下，注意力内核的输入张量形状（即 Query token 数量 与 Key/Value token 数量）。最后，我们对注意力内核时延进行预测，并选择 注意力计算时延更低 的 CP 分片策略。

为准确估计注意力内核时延，我们利用了 §5.2 中得到的关键洞见。首先，我们计算注意力计算所需的 总浮点运算量。同时，考虑内核层面的填充开销，将文档 chunk 填充到 tile 大小的整数倍。接着，我们基于 离线性能剖析 所收集的数据，估计在给定张量形状下可实现的 TFLOPs，其中包含 TMA 使用效果 的影响。最后，通过将浮点运算量除以实现的 TFLOPs，得到注意力内核的时延估计。通过这种 自适应 CP 分片选择，WLB-LLM 能够最小化 CP 层级的训练时延。

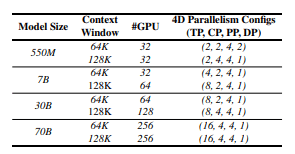表 1： 模型与 4D 并行配置。

实现细节

WLB-LLM 构建于一种被广泛采用的 4D 并行训练范式 之上，在每一个并行层级都集成了先进的分布式训练技术。在 数据并行（DP） 层面，WLB-LLM 使用 FSDP，该方法在 DP 工作节点之间均匀切分模型参数，相比传统 DP 方法显著降低了内存需求。在 流水线并行（PP） 层面，WLB-LLM 采用 交错式 1F1B 流水线调度。为支持 可变长度打包优化，WLB-LLM 进一步实现了 可变长度流水线，使 micro-batch 可以具有不同的序列长度。

在 上下文并行（CP） 层面，逐序列分片的基线方案遵循 Llama3 训练中采用的 基于 AllGather 的 CP 方法，在前向传播阶段通过 AllGather 收集完整的 KV 张量以进行注意力计算。在此基础上，WLB-LLM 通过优化 文档划分与分发，实现了 细粒度逐文档分片。在 张量并行（TP） 层面，WLB-LLM 采用 一维张量并行，并启用 序列并行。此外，WLB-LLM 还引入了 计算–通信重叠 机制，以进一步提升 TP 层级的训练性能。

评估

在本节中，我们在多种 LLM 模型规模 与 4D 并行配置 下对 WLB-LLM 进行了评估，模型规模从 550M 到 70B 不等。我们首先展示了 端到端训练时延 的改进效果。随后，分别分析了 PP 层级优化（§4）和 CP 层级优化（§5）对整体加速比的贡献。最后，通过对比 训练损失曲线，验证 WLB-LLM 的优化不会损害模型质量或模型收敛性。

实验设置

硬件环境：我们在一个包含 32 个节点 的集群上部署 WLB-LLM。每个节点配备 8 张 NVIDIA H100 SXM 80GB GPU，节点内通过 高带宽 NVLink 互联，节点间通信则通过 RoCE 实现。

图 12： 在多种配置下，WLB-LLM 与 Fixed-4D 相对于 Plain-4D 的训练性能加速比。

模型与并行配置

我们在一系列内部 类 LLaMA 模型 上进行了实验，覆盖四种不同规模：550M、7B、30B 和 70B。其中，7B 模型与 LLaMA2-7B 模型采用相同架构，其余模型在保持架构一致的前提下，按比例调整层数与模型维度大小。对于每一种模型规模，我们分别评估了两种 上下文窗口大小：64K 和 128K。

每种模型规模与上下文窗口大小均对应一个特定的 4D 并行配置。全局 batch 大小设置为 PP_size × DP_size，所有实验均使用 bfloat16 精度。训练设置与并行配置的详细信息见 表 1。在将 4D 并行映射到硬件时，内层并行维度（如 TP 或 CP）优先映射到 节点内 GPU，以充分利用 NVLink 的高带宽通信；外层并行维度（如 DP）则映射到 跨节点 的 GPU。

在本文其余部分，我们使用 模型规模–上下文窗口大小 来表示具体配置。例如，7B-128K 表示 7B 模型、128K 上下文窗口。

基线方法

我们将 WLB-LLM 与以下两种基线方法进行对比：

• Plain-4D：这是我们用于大规模 LLM 训练的内部代码库，支持 4D 并行，可扩展至 10 万张 GPU。Plain-4D 直接使用数据加载器生成的输入 batch 进行训练，不对输入打包进行优化。在 CP 分片方面，Plain-4D 采用 逐序列分片 方法，即在 整个序列层面 对输入序列进行分片。

• Fixed-4D：Fixed-4D 应用了 §3.2 中描述的 固定长度打包 基线优化。为最小化打包开销，该方法使用 贪心算法 替代求解器，并将打包范围限制在 单个全局 batch 内，以保持数据加载随机性并避免训练损失上升。在 CP 分片方面，Fixed-4D 在整个训练过程中固定使用 逐序列分片 或 逐文档分片 之一，并在两种策略中选择性能更优的结果用于对比。

训练性能

我们在不同 模型规模 与 上下文窗口大小 组合下，对 WLB-LLM 及所有基线方法进行了评估。

Plain-4D 与 Fixed-4D 对比

如 图 12 所示，Fixed-4D 相较 Plain-4D 仅取得了 有限的性能提升，在所有设置下的平均加速比约为 1.03×。这一增益有限的主要原因在于：Fixed-4D 仅在 单个全局 batch 内调整文档打包，并受到 上下文窗口大小 的限制，无法有效处理 极长异常文档（例如长度等于上下文窗口大小的文档）。由于注意力计算随文档长度呈 平方级增长，在上下文窗口约束下，将多个短文档打包在一起，无法匹配单个极长文档的计算负载。

此外，Fixed-4D 在 CP 层级对所有输入 batch 固定采用 逐序列分片 或 逐文档分片，忽略了 注意力内核效率 与 分片均衡性 之间的权衡，导致整体性能并不理想。这些局限性共同限制了 Fixed-4D 相对于 Plain-4D 的性能提升。

WLB-LLM 与基线方法对比

如 图 12 所示，WLB-LLM 在不同模型规模与 4D 并行配置下 始终优于所有基线方法。具体而言，WLB-LLM 相较 Plain-4D 和 Fixed-4D 分别实现了 1.23× 和 1.19× 的加速比。

这一显著提升主要源于 WLB-LLM 的两项关键优化： 在 PP 层级，WLB-LLM 采用 启发式可变长度文档打包算法，不再受限于固定上下文窗口大小，并通过 选择性延迟异常文档 的方式，相比固定长度打包实现了更高程度的工作负载平衡。 在 CP 层级，WLB-LLM 结合 逐序列分片 与 逐文档分片，并为每个 micro-batch 自适应选择最优分片策略，从而最大化整体性能。

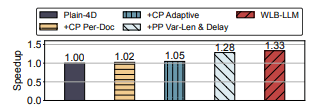图 13： 在 7B-128K 配置下，WLB-LLM 的性能分解结果。

不同模型规模与上下文窗口大小下的表现

如 图 12 所示，随着模型规模增大，WLB-LLM 的加速比略有下降。这是因为更大的模型通常需要使用 更多 GPU 进行训练，从而提高了 通信时延 在总时延中的占比，使得注意力层中工作负载不均衡的影响相对减弱。

相反，将上下文窗口大小从 64K 提升到 128K，平均加速比从 1.15× 提高到 1.30×。这是因为 更长的上下文 会进一步加剧工作负载不均衡问题，从而放大 WLB-LLM 优化的收益。关于上下文窗口大小的更详细敏感性分析将在 §7.3 中给出。

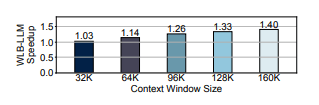图 14： 在 7B 模型 上，不同上下文窗口大小下 WLB-LLM 的加速比。

性能分解与敏感性分析

在本节中，我们对 WLB-LLM 进行了 性能分解 与 敏感性分析。具体而言，我们首先通过性能分解评估各项优化技术的影响；随后，通过改变上下文窗口大小来分析加速比的敏感性。

加速比分解

我们在 图 13 中展示了 7B-128K 训练配置下的加速比分解结果，方法是将 WLB-LLM 中提出的各项优化技术分别应用到 Plain-4D 上。通过在 CP 层级采用 细粒度逐文档分片，由于 CP 工作节点之间的不均衡得到缓解，我们观察到 1.02× 的加速。然而，该加速幅度较为有限，这是由于 内核效率 与 分片均衡性 之间的权衡所致。因此，逐文档分片并非在所有情况下都有利，甚至可能导致性能下降。

通过 自适应地选择逐文档分片与逐序列分片策略，加速比可进一步提升至 1.05×。随后，我们将 PP 层级的优化应用于 Plain-4D，以分析其影响。可以观察到，将 启发式可变长度打包 与 异常文档延迟 相结合，能够带来显著的 1.28× 加速。最后，我们同时引入 CP 与 PP 层级的优化，在所有并行层级上最大程度地降低工作负载不均衡，从而实现最终 1.33× 的加速。

不同上下文窗口大小下的加速比

我们进一步研究了 上下文窗口大小 对 WLB-LLM 性能提升的影响。图 14 展示了在 7B 模型 上、上下文窗口大小从 32K 到 160K 变化时，相对于 Plain-4D 的加速比。可以观察到，随着上下文窗口增大，加速效果愈加显著，在 160K 上下文窗口下可达到 1.40× 的加速。

这是因为更大的上下文窗口会提高 异常文档 出现的概率；同时，上下文窗口越大，注意力计算 在整体训练时延中的占比也越高，从而放大了不均衡对训练时延的影响。加速比随上下文窗口增大的趋势，充分表明了 WLB-LLM 在应对当今不断扩展的上下文窗口规模方面具有显著潜力。

优化分析

在本节中，我们首先分析 WLB-LLM 中 打包 与 分片 优化的有效性；随后，验证系统级优化不会损害模型质量或减缓模型收敛。

打包平衡性与开销分析

为评估不同打包策略下 micro-batch 之间计算工作负载的平衡程度，我们在 7B-128K 训练任务中，对采用不同打包方法与配置时 每个 micro-batch 的前向传播时延 进行了剖析与对比。如 §3.1 所述，PP 层级的时延主要由 最大 micro-batch 决定。因此，我们使用如下指标来表示一个 batch 的不均衡程度：

$$ \frac{\text{Max_Latency} \times PP_size}{\text{Total_Latency}} $$

其中，Max_Latency 表示 最大 micro-batch 的前向时延，Total_Latency 表示 所有 micro-batch 的前向时延之和。不均衡度越低，说明该 batch 在工作负载方面越均衡。

不同方法下的不均衡度以及 打包开销（即 每个 batch 的打包时延）结果如 表 2 所示。我们评估了四种不同的打包方法：

（1）Original Packing：直接使用数据加载器生成的原始输入 batch； （2）Fixed-Len Greedy：Fixed-4D 基线中使用的方法，在若干全局 batch 内以 贪心方式 打乱文档，以优化 micro-batch 之间的工作负载平衡； （3）Fixed-Len Solver：使用 ILP 求解器 求解式 (1)，在给定全局 batch 的基础上获得 最优固定长度打包方案； （4）WLB-LLM：采用 可变长度打包 并结合 异常文档延迟 的方法。

此外，我们还展示了在 不同异常文档队列数量 下 WLB-LLM 的性能表现。

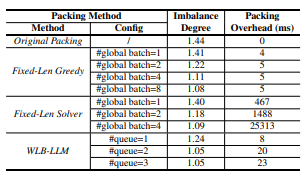表 2： 打包不均衡度与打包开销分析。

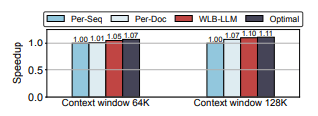图 15： CP 分片性能对比。

打包与分片优化分析

如 表 2 所示，当仅在 单个全局 batch 内进行打包时，Fixed-Len Greedy 只能在一定程度上缓解工作负载不均衡。若跨多个全局 batch 进行打包，可以实现 更低的不均衡度，但会带来 更高的训练损失，如 图 6 所示。对于 Fixed-Len Solver，在相同全局 batch 数量下，其不均衡度低于 Fixed-Len Greedy。然而，基于求解器的方法存在 显著的打包开销。例如，当跨 4 个全局 batch 进行打包时，每个 batch 的平均打包时延超过 25 秒。

相比之下，WLB-LLM 是唯一同时实现 近似最优不均衡度 与 低打包开销 的方案。例如，在使用 两个异常文档队列 时，WLB-LLM 达到 1.05 的不均衡度。此外，其 单 batch 打包时延 仅为 20 ms，相较于 单步训练时延 仅占 0.65% 以下。

CP 分片性能分析

为验证 WLB-LLM 在 CP 层级中 逐文档分片 及 自适应分片选择 优化的有效性，我们在一个 CP 大小为 4 的 7B 模型单个 Transformer 层 上进行了案例研究。我们对比了以下分片策略下的 前向与反向传播时延：

（1）逐序列分片（Per-Seq）； （2）逐文档分片（Per-Doc）； （3）WLB-LLM：根据给定 micro-batch 在运行时于 Per-Seq 与 Per-Doc 之间 自适应选择； （4）Optimal：始终在 Per-Seq 与 Per-Doc 中选择 时延更低 的最优结果。

如 图 15 所示，在 64K 与 128K 上下文窗口下，逐文档分片相较逐序列分片分别实现了 1.01× 与 1.07× 的加速，验证了逐文档分片在缓解 CP 层级工作负载不均衡方面的有效性。然而，细粒度逐文档分片 可能会牺牲 注意力内核效率，尤其是在输入序列由大量短文档组成时。

为克服这一问题，WLB-LLM 采用 自适应分片选择方法，在运行时为每个 micro-batch 智能选择更优的分片策略。图 15 的结果表明，WLB-LLM 相较 静态 Per-Seq 与 静态 Per-Doc 分片，分别实现了 7.5% 与 3.4% 的性能提升。此外，WLB-LLM 的性能非常接近 最优结果，充分证明了该自适应选择方法的有效性。

模型收敛性分析

WLB-LLM 使用了一种 启发式可变长度打包优化，会调整文档打包方式并延迟异常文档的执行。为证明该优化不会影响模型收敛性，我们给出了 550M 模型 的训练损失曲线。

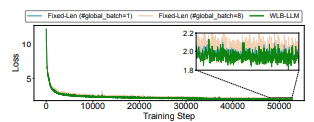图 16： 550M 模型上的训练损失对比。

如 图 16 所示，当跨 8 个全局 batch 进行打包时，训练损失出现了明显上升（平均 1.6%）。这是因为跨多个全局 batch 的打包会破坏数据加载器中的 数据采样随机性，导致每个 batch 的数据分布偏离预期。相比之下，WLB-LLM 的训练损失曲线几乎与 单全局 batch 的固定长度打包 保持一致。这是由于 WLB-LLM 使用的启发式可变长度打包算法 仅延迟异常文档，而这些文档只贡献了 极少比例的输入 token。

根据我们的性能剖析，在 WLB-LLM 中，每个 token 平均仅被延迟 0.5 次迭代。这种 极小的延迟 最大程度地保持了原始数据分布，使 WLB-LLM 能够在 不牺牲模型质量 的前提下显著提升训练效率。

讨论

在本节中，我们讨论 WLB-LLM 与其他并行维度的兼容性，以及未来可能的优化方向。

与专家并行的兼容性

除 4D 并行 外，专家并行（Expert Parallelism，EP） 是一种面向 混合专家模型（MoE） 的互补并行维度。在 EP 中，不同专家被分布到不同工作节点上，每个输入 token 会在运行时独立路由到一个或多个专家。当专家容量被超过时，可能引入负载不均衡问题。已有工作通过 负载均衡辅助损失 或 在路由分数中注入专家偏置 来缓解该问题。借助这些优化，当前最先进的 MoE 训练已经实现了 无丢弃（dropless）的 token 路由，确保所有 token 都严格依据其 gating logits 被分发，而不会因容量限制被丢弃。

在这种背景下，WLB-LLM 的打包与分片优化不会影响 EP 的路由决策，使其能够与现有的 EP 负载均衡策略 完全兼容。

进一步优化的机会

WLB-LLM 中的 自适应 CP 分片选择 是在 整个输入序列粒度 上进行的，即对完整序列选择 逐序列分片 或 逐文档分片 之一。尽管该方法已经实现了 接近最优的性能，但仍存在进一步优化的空间。

在某些场景下，例如输入序列同时包含 极长文档 与 大量短文档 时，可能更适合 组合使用 两种分片策略，并根据文档长度进行选择性应用。例如，可以对 长文档 使用逐文档分片以平衡工作负载，而对 短文档 使用逐序列分片以最大化注意力内核效率。我们希望这一观察能够激发未来的研究工作，进一步提升 CP 训练的整体效率。

相关工作

分布式 LLM 训练框架

为应对训练超大规模 LLM 的挑战，先前工作主要依赖 3D 并行，即将 张量并行、流水线并行 和 数据并行 相结合。尽管 3D 并行 已被证明在 模型规模扩展 方面行之有效，使得训练 万亿参数规模 的模型成为可能，但其在 上下文窗口规模 的扩展上表现受限。

为解决这一局限，引入了一种新的并行维度——上下文并行，从而形成 4D 并行训练范式。上下文并行通过将输入序列拆分为多个 chunk，有效缓解了 极长文档 带来的内存瓶颈。早期的上下文并行采用 基于环的方式，通过 P2P 通信 实现通信与计算的重叠。近期方法则利用 集合通信（如 AllGather 或 AlltoAll）来聚合 Key 和 Value 张量，在支持多种注意力掩码方面具有更高的灵活性。

上下文并行的引入，使得 长上下文窗口 LLM 的高效训练成为可能。然而，现有 4D 并行框架 忽略了 逐 token 算术强度的异构性，从而导致 GPU 之间出现显著的 工作负载不均衡。

LLM 训练中的输入填充与打包

LLM 的输入由 长度不一的样本 构成。为了在训练过程中实现批处理并提升 GPU 利用率，必须将输入文档组织为 长度一致的张量。主要有两种实现方式：填充（Padding） 与 打包（Packing）。

填充通过在 micro-batch 中对较短文档添加 零填充 来实现长度对齐，但这种方式不可避免地引入 冗余计算、通信与内存开销。为缓解该问题，已有工作设计了更高效的内核以减少冗余计算，或通过优化批处理策略来最小化填充开销。然而，填充带来的额外成本无法被完全消除。

为进一步解决该问题，近期研究提出将 多个短文档打包 为一个长输入序列。打包之后，需要额外的 注意力掩码，以确保 token 仅在同一文档内部进行注意力计算。由于能够有效避免冗余计算，打包 已成为 LLM 训练中的主流选择。例如，LLaMA3 在训练中采用了输入打包，而最新的高性能注意力实现（如 FlashAttention）也支持在文档打包场景下的高效注意力计算。

WLB-LLM 聚焦于 输入打包，并针对文档打包后所引入的 工作负载不均衡问题 提供了系统性的解决方案。

总结

本文提出了 WLB-LLM，一种 工作负载均衡的 4D 并行训练框架，旨在提升大语言模型训练的整体效率。WLB-LLM 系统性地识别并解决了在多个并行层级中出现的工作负载不均衡问题。

在 流水线并行 层级，WLB-LLM 提出了一种 启发式可变长度文档打包算法，并结合 异常文档延迟方法，有效缓解了 micro-batch 之间的工作负载不均衡。在 上下文并行 层级，WLB-LLM 设计了 细粒度逐文档分片方法，并引入 自适应分片选择策略，以最大化 CP 训练效率。

大量实验结果表明，WLB-LLM 在多种模型规模与并行配置下均优于现有的 4D 并行训练框架，并实现了 平均 1.23× 的训练加速比。