阅读MLAI

FSMoE：一种用于稀疏混合专家模型的灵活且可扩展的训练系统

发布于 • 作者: Xinglin Pan et al.

摘要

近年来，大型语言模型（LLMs）倾向于利用稀疏性来减少计算量，常用的方法是采用*稀疏激活的混合专家（Mixture-of-Experts, MoE）*技术。MoE 引入了四个模块，包括令牌路由（token routing）、令牌通信（token communication）、专家计算（expert computation）以及专家并行（expert parallelism），这些模块都会影响模型质量和训练效率。为了实现 MoE 模型的多样化使用，我们提出了 FSMoE，一种通过三项新技术来优化任务调度的灵活训练系统： 1）对 MoE 模块进行统一抽象与在线性能分析，从而支持跨多种 MoE 实现的任务调度； 2）将节点内与节点间通信与计算进行协同调度，以最小化通信开销； 3）为支持近似最优的任务调度，我们设计了一种自适应梯度分区方法用于梯度聚合，并提出了一种自适应流水化通信与计算的调度方案。

我们在两个 GPU 集群上，使用配置化 MoE 层和真实世界 MoE 模型进行了大量实验。实验结果表明： 1）FSMoE 支持四种主流的 MoE 路由函数，并且相比现有实现更加高效（最高可达 1.42× 的加速）； 2）在 1458 个 MoE 层配置上，FSMoE 相比当前最先进的 MoE 训练系统（DeepSpeed-MoE 和 Tutel）实现了 1.18×–1.22× 的性能提升；在基于 GPT-2 和 Mixtral、并使用主流路由函数的真实 MoE 模型上，实现了 1.19×–3.01× 的加速。

CCS 概念

• 计算方法学 → 并行算法；机器学习。

关键词

分布式深度学习；大型语言模型；混合专家；训练系统；调度

引言

近年来，稀疏激活的混合专家（MoE）层在大型语言模型（LLMs）中受到了广泛关注，因为 MoE 能够在保持训练计算成本次线性增长的同时，大幅扩展模型规模。MoE 模型在 MoE 层中引入多个专家（experts），每个专家通常是一个针对特定子任务（对应特定输入令牌）训练的前馈网络（FFN）。这些 MoE 层通过一种门控机制（gating mechanism），利用路由函数（例如采用 softmax 激活）将数据样本动态分配给合适的专家，从而实现模型规模的扩展。

例如，Switch Transformer 将模型规模扩展至 1.5 万亿参数，其包含 15 个 MoE 层，每个 MoE 层由 2048 个专家组成，显著超越了其不含 MoE 的稠密模型（仅有数十亿参数）。MoE 技术已在自然语言处理、计算机视觉、语音识别以及推荐系统等领域显著提升了模型性能。

尽管 MoE 技术在众多 AI 模型中取得了巨大成功，但在算法和系统层面仍然是一个活跃的研究方向。从算法角度来看，如何高效、有效地使用输入令牌来训练专家仍是一个开放问题，这意味着路由函数在模型泛化能力中起着至关重要的作用。从系统角度来看，已经出现了多种专用的 MoE 系统（例如 FastMoE、DeepSpeed-MoE、FlexMoE、Tutel 和 ScheMoE），用于支持 MoE 算法研究和模型部署。

在这些系统之上，还提出了大量优化策略来提升 MoE 训练效率，例如：

  • 设计高效的通信集合操作（如 All-to-All 算法），
  • 优化稀疏计算，
  • 通过调度通信与计算任务，实现通信与计算的重叠。

然而，这些系统主要存在两个局限性： 1）仅支持有限类型的路由函数，难以灵活支持新引入的路由机制； 2）通常针对特定并行方式进行优化，在一些常见场景下并非最优。

随着 LLM 规模的不断扩大，为应对日益增长的计算需求，出现了多种并行范式。除传统模型中广泛使用的三种并行方式——数据并行（DP）、模型并行（MP） 和 流水线并行（PP） 之外，MoE 模型还引入了两种新的并行范式：专家并行（EP）和专家切分并行（ESP），以支持在 GPU 集群上训练大规模专家网络。这些并行方式通过引入额外通信，显著影响系统的可扩展性。

已有研究表明，在高端 GPU 或 TPU 集群上执行 MoE 层时，All-to-All 通信时间可占整体执行时间的 30%–60%。当在大规模训练中同时采用 DP、MP、EP 和 ESP（即 DP+MP+EP+ESP）时，这一问题将更加严重。因此，快速变化的 MoE 路由机制和复杂的并行方式，在系统设计上既带来了模块化支持的挑战，也带来了任务调度性能优化的挑战。

为此，本文提出 FSMoE，一种具有近似最优任务调度能力的灵活高效 MoE 训练系统。

  • 首先，为提升可扩展性，我们对 MoE 模块进行了统一抽象并引入在线性能分析，以支持多种 MoE 实现的任务调度。
  • 其次，为更好地调度 DP+MP+EP+ESP 场景下的通信与计算任务，我们分析了节点内与节点间通信重叠的可能性，并在 MP 与 ESP 分组数量与单节点 GPU 数量一致的常见场景下，提出了一种高效的流水化调度方案。
  • 第三，为实现近似最优的任务调度，我们设计了一种梯度分区方法，用于将梯度聚合与其他任务完全重叠。

本文的主要技术贡献如下：

  • 我们对 MoE 层中的所有可能操作进行了模块化，以支持多种 MoE 组件，包括门控函数、数据布局、集合通信和专家计算等，并在系统中实现了四种主流门控函数，其性能优于原始实现。
  • 基于模块化操作，我们提出了一种自适应最优调度算法，能够在 MP 与 ESP 分组数量等于单节点 GPU 数量的常见场景下，对节点内与节点间通信及计算任务进行流水化调度，从而提升训练效率。
  • 我们设计了一种自适应梯度分区方法，通过将梯度聚合通信与计算流水化，隐藏梯度聚合的通信开销，并避免不同节点间通信之间的资源竞争。
  • 我们在一个 48-GPU 集群和一个 32-GPU 集群上，使用定制 MoE 层和真实世界 MoE 模型进行了大量实验。实验结果表明： 1）在 1458 种不同配置的训练场景中，FSMoE 相比 Tutel（及其改进算法 PipeMoE）实现了 1.18×–1.22× 的性能提升； 2）在基于 GPT-2 和 Mixtral 的两个真实世界 MoE 模型训练中，FSMoE 相比当前最先进的 MoE 系统（Tutel 和 DeepSpeed-MoE）平均加速 1.19×–3.01×。

背景与动机

为便于说明，我们在 表 1 中总结了本文中使用的关键符号。

符号 / 名称 含义说明
P GPU 数量
r 流水线并行度（Pipeline Degree）
B 每个 GPU 的样本数（本地 mini-batch 大小）
L 每个样本的 Token 数（序列长度）
E 专家（Expert）总数
k 每个 Token 选择的 Top-k 专家数量
f 控制专家最大 Token 数量的系数
M Token 的嵌入维度（Embedding Size）
H 专家中前馈网络（FFN）的隐藏层维度
N_head 注意力层中的头数（Number of Heads）
N_DP 每个数据并行（DP）组中的 Worker 数量
N_MP 每个模型并行（MP）组中的 Worker 数量
N_EP 每个专家并行（EP）组中的 Worker 数量
N_ESP 每个专家切分并行（ESP）组中的 Worker 数量
N_PP 每个流水线并行（PP）组中的 Worker 数量

表 1：符号说明。

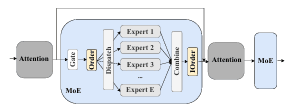fsmoe-0 图 1：包含 $E$ 个专家的典型 MoE 结构。

混合专家层

在现代 MoE 模型中，这类模型通常构建于 Transformer 架构之上，MoE 层被用来替代前馈网络（ffn）层。如图 1 所示，一个 MoE 层由三个核心组件组成：门控函数（gating function）、排序函数（ordering function）（及其逆操作，即 I-ordering 函数）以及一组包含 $E$ 个专家（experts）。

门控函数

门控函数在将令牌分配给特定专家的过程中起着关键作用。在每一次训练迭代中，MoE 层的输入数据（记为 $I$）的形状为 $(B, L, M)$，其中 $B$ 表示小批量大小，$L$ 表示每个样本的序列长度，$M$ 表示嵌入维度大小。为了确定哪些专家被激活，输入 $I$ 会根据门控函数被划分为多个部分。

GShard 使用一种带噪声的 Top-$k$ 门控（noisy Top-$k$ Gate），记为 $$ G(I) = \mathrm{Softmax}(\mathrm{KeepTopK}(H(I), k)), $$ 其中 $H(I)$ 通过特定变换向输入 $I$ 中注入噪声： $$ H(I)_i = I \cdot W_g{}i + \mathcal{N}(0,1)\cdot \mathrm{Softplus}\big((I \cdot W{\text{noise}})_i\big), $$ 函数 $\mathrm{KeepTopK}(v, k)$ 会保留向量 $v$ 中最大的 $k$ 个元素，其余元素置为负无穷： $$ \mathrm{KeepTopK}(v,k)i = \begin{cases} v_i, & \text{若 } v_i \text{ 位于 } v \text{ 的前 } k \text{ 大值中}
-\infty, & \text{否则} \end{cases} $$ 其中 $W_g$ 和 $W{\text{noise}}$ 是两个可训练参数矩阵。

在 BASE 和 StableMoE 模型中，采用了 sigmoid 门控，其定义为 $$ H(I)_i = (I \cdot W_g)_i。 $$ 专家的输出会乘以 $\sigma(H(I)_i)$ 进行缩放。如果该输出对 $I$ 有正向贡献，从而优化训练目标（例如语言建模中的交叉熵损失最小化），则门控值会被增大，从而更倾向于再次选择同一个专家。

在 X-MoE 中，使用了一个低秩线性投影 $W_{\text{proj}} I$，用于隔离隐藏向量 $I$ 与专家嵌入 $W_g$ 之间的直接交互，从而有效缓解表示级联坍塌问题。随后，这些表示会经过 $l_2$ 归一化进行缩放，其形式为： $$ s_i = \cos(W_{\text{proj}} I, W_g)。 $$ Expert Choice 方法会为每个专家独立选择 Top-$k$ 个令牌，其门控定义为： $$ G(I) = \mathrm{Softmax}\big(\mathrm{KeepTopK}((I \cdot W_g)^\top, k)\big)。 $$

门控函数的有效性通常需要在特定模型和数据集上进行评估。例如，EC 在因果语言建模任务中进行评估，而 X-MoE 则在掩码语言建模任务中进行评估。当面对新的应用场景时，开发者往往无法在不进行实际实验的情况下判断哪种门控函数最适合。因此，支持多样化的门控函数对于提升系统的鲁棒性至关重要。

排序函数与 I-排序函数

排序函数在分发之前对输入张量的数据布局进行转换，通常会将格式从 $(B, L, M)$ 转换为 $(E, T, M)$，其中 $T$ 表示每个专家可处理的最大令牌数。$T$ 的计算公式为： $$ T := k \times f \times B \times L / E, $$ 其中 $f$ 是一个控制因子。张量 $G$ 的每一行（即 $G[i, :, :]$）对应第 $i$ 个专家（$i = 1, \dots, E$）的数据。

排序函数主要有两种类型： 1）GShard 排序，基于 einsum 与矩阵乘法的组合实现； 2）Tutel 排序，采用对 SIMT 架构高效的稀疏操作实现。

I-排序函数是排序函数的逆操作，用于将数据布局恢复为原始格式。

专家

通常，MoE 层中的每个专家都是一个紧凑的神经网络，由若干前馈层和激活函数组成。以一个两层专家为例，其第一层权重矩阵形状为 $(M, H)$，第二层权重矩阵形状为 $(H, M)$，其中 $H$ 表示隐藏层维度，因此专家输出的形状与输入保持一致。

对于包含 $E$ 个专家的 MoE 层，第 $i$ 个专家记为 $e_i$，其输出可表示为： $$ Q_i = e_i(G[i, :, :])。 $$ 为了获得 MoE 层的最终输出，需要将所有专家的输出合并为一个统一的张量 $[Q_1, Q_2, \dots, Q_E]$，并重新 reshape 为 $(B, L, M)$，以便传递给后续网络层。

尽管 MoE 模型在参数规模上大幅扩展，其计算成本的增加却相对有限。然而，模型规模已经增长到无法加载到单个设备内存中的程度，因此必须采用分布式训练来满足计算与内存需求，这也不可避免地引入了显著的通信开销。我们在 32-GPU 与 48-GPU 测试平台上，对两个主流 MoE 模型的训练时间分解进行了基准测试（细节见第 6 节），结果如表 2 所示。结果表明，通信开销通常占据超过 50% 的总体训练时间，凸显了优化通信性能的必要性。

并行范式

为了在 GPU 集群上训练大规模 MoE 模型，需要结合 DP、MP、EP 和 ESP 的混合并行策略。

数据并行

在分布式深度学习中，数据并行（DP） 是一种事实上的标准方法。在 DP 中，一个小批量样本会被分配到 DP 组内的多个工作节点。在反向传播阶段，同一 DP 组内各工作节点的梯度会通过一次 AllReduce 操作进行聚合（下文称为 Gradient-AllReduce），从而使用相同的梯度来更新模型参数。

模型并行

模型并行（MP）通过将模型参数划分到多个工作节点上来实现并行计算。每个节点独立执行计算，随后通过 AllReduce 集合通信操作对所有节点的输出进行合并。值得注意的是，当 MP 组的规模与单节点 GPU 数量一致（这是非常常见的配置）时，MP 所涉及的通信主要是节点内通信，而梯度聚合所需的集合通信则涉及节点间通信。

专家并行

在 专家并行（EP） 中，不同专家被分配到不同 GPU 上，每个设备负责一部分专家。在门控函数之后，张量 $G$ 的各行（$G[i, :, :]$）对应第 $i$ 个专家的数据。由于专家分布在多个设备上，分发操作需要通过一种称为 AlltoAll Dispatch 的集合通信来将令牌发送至对应专家。随后，所有专家生成的输出会通过另一轮 AlltoAll Combine 操作进行汇总。

专家切分并行

在训练大规模 MoE 模型时，工作节点数 $P$ 可能超过专家数 $E$。此时，可以采用 专家切分并行（ESP），将专家均匀划分到 ESP 组内的多个 GPU 上，类似于模型并行，从而在 ESP 组内实现专家计算的并行化。

EP 与 ESP 的结合使得单个 MoE 层可以分布在多个 GPU 上执行，但同时也引入了额外的通信算子，即 ESP-AllGather 和 ESP-ReduceScatter。其中，ESP-AllGather 用于在 ESP 组内均匀分发输入数据，而 ESP-ReduceScatter 则用于聚合专家分片的输出并将其还原到原始结构。ESP 组中的 GPU 数量记为 $N_{\text{ESP}}$。当 ESP 组配置为单节点内的 GPU 数量时，ESP-AllGather 和 ESP-ReduceScatter 属于节点内通信，而 EP 引入的 AlltoAll 则是节点间通信，从而可以实现二者的重叠。本文主要讨论这一配置下的调度策略。

一个结合 DP、MP、EP 和 ESP 的 MoE 模型训练示例如图 2 所示，其中 $N_{\text{DP}} = N_{\text{MP}} = N_{\text{EP}} = N_{\text{ESP}} = 2$。可以看到，训练过程中涉及多个关键组件和复杂的并行交互，这正是我们设计灵活、可扩展 MoE 训练系统的动机。

动机

灵活的 MoE 框架

一个灵活的 MoE 框架应当能够高效地组合不同的路由函数、排序函数、专家模块以及 AlltoAll 算法，并且在进行额外定制时不应引入复杂的编程负担。其目标是在同时集成 DP、MP、EP 和 ESP 等多种并行组的情况下，全面支持通信与通信之间、通信与计算之间等各种重叠场景，从而实现高效的 MoE 训练。

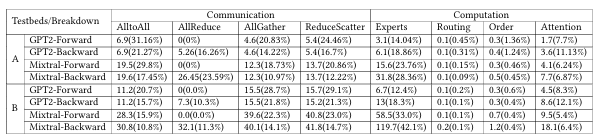fsmoe-1 表 2：两个真实世界模型（GPT2-XL 和 Mixtral 7B）在 Transformer 层中各操作的时间性能（单位：毫秒）。括号中的数值表示各操作在前向与反向传播时间中所占的比例。

fsmoe-2 图 2：一个 $N_{\text{DP}} = N_{\text{MP}} = N_{\text{EP}} = N_{\text{ESP}} = 2$ 的示例。注意力层在 MP 组之间被划分为两部分；在 EP 中，两个专家被分配到两个 EP 组（GPU1 与 GPU3，以及 GPU2 与 GPU4）；并且每个专家在 ESP 组中进一步被切分为两个分片。蓝色与绿色矩形表示数据张量。

优化网络通信

为缓解 MoE 层带来的通信开销，先前研究（如 Tutel、PipeMoE、Faster MoE）探索了将 AlltoAll 与专家计算进行重叠，如图 3b 所示。然而，这些工作并未探索将 ESP-AllGather / ESP-ReduceScatter（节点内通信） 与 AlltoAll Dispatch / Combine（节点间通信） 进行重叠，从而限制了网络效率。这一问题促使我们提出如图 3c 所示的方案，将节点间通信与节点内通信进行流水化（见第 4 节）。

前向与反向过程的独立优化

现有系统（如 Tutel 和 DeepSpeed-MoE）通常在训练过程中，对前向传播与反向传播采用相同的流水化深度（即用于重叠的输入切分块数量）。然而，由于两者的计算需求不同，理想的流水化深度可能并不一致。例如，反向传播还需要额外计算权重梯度。我们在 1458 种 MoE 配置上的大量实验（见表 4），在一个包含 8 个节点的 32-GPU 集群上表明，其中 912 种配置在前向与反向阶段具有不同的最优流水化深度。因此，需要自适应地为前向与反向阶段确定流水化深度，以获得更高的训练效率（见第 4.4 节）。

反向传播与梯度同步的协同设计

由于 Gradient-AllReduce（由 DP 中的权重同步引入）与 AlltoAll 均属于节点间通信，Gradient-AllReduce 无法与整个 MoE 层直接重叠。如图 3b 与图 3c 所示，现有方法仅能将 Gradient-AllReduce 与非 MoE 部分重叠。因此，在不考虑 MoE 层的情况下设计 Gradient-AllReduce 的重叠策略，往往会导致次优解。一种同时考虑 AlltoAll 操作并通过调整梯度分区以实现最优重叠的协同设计方案，仍有待探索（见第 5 节）。

FSMoE：系统设计

我们提出 FSMoE，一种用于分布式训练的灵活且可扩展的 MoE 框架。该框架具有三项主要特征： 1）模块化与非侵入式修改； 2）前端 API 定义与后端任务调度的隔离； 3）不同任务的易调度性。

模块化与非侵入式修改

在 FSMoE 框架中，MoE 层被划分为六个相互独立的子模块：Gate、Order、I-Order、Dispatch、Combine、Expert。

Gate：Gate 子模块决定令牌如何被分配给不同专家进行计算。我们预实现了四种路由函数：GShard 路由、Sigmoid 路由、X-MoE 路由以及 SoftMoE 路由。

Order 与 I-Order：Order 子模块在分发前对输入张量的数据布局进行转换，通常从 $(B, L, M)$ 变为 $(E, T, M)$。我们预实现了两种排序函数： 1）GShard 排序，基于 einsum 与矩阵乘法的组合； 2）Tutel 排序，采用对 SIMT 架构高效的稀疏操作。 I-Order 子模块是 Order 的逆操作，用于将数据布局恢复为原始形式。

Dispatch 与 Combine：Dispatch 子模块负责令牌到专家分发的集合通信。用户可以在不影响调度器的情况下，自定义集合通信算法。为此，我们预实现了多种方案，包括 NCCL-A2A、Hetu 提出的 1DH-A2A，以及 Tutel 和 DeepSpeed-MoE 提出的 2DH-A2A。这种可定制性确保了能够根据用户需求实现最优分发。Combine 子模块是 Dispatch 的逆操作。

Expert：Expert 子模块负责计算任务。任何继承自 torch.nn.Module 的模块都可以作为专家组件。我们提供了两种实现：GPT 前馈网络与 Mixtral 前馈网络。

Hooks：框架提供了一系列用于非侵入式修改的钩子，包括 BeforeMoeStartHook、BeforeDispatchHook、AfterDispatchHook、BeforeCombineHook、AfterCombineHook 以及 BeforeMoeEndHook。这些钩子可在无需修改核心代码的情况下完成多种扩展。例如，在多模态场景中，可使用 BeforeMoeStartHook 与 BeforeMoeEndHook 重新格式化输入；在通信压缩场景中，可使用 BeforeDispatchHook 进行压缩，并在 AfterDispatchHook 中解压。

通用调度器

FSMoE 提供了独立于具体 API 定义的通用流水化调度能力，并内置性能分析器，用于评估不同任务的执行时间。通过数据采集与预测建模，调度器能够在 MoE 子模块层面进行协调，以实现更高效率。系统由前端与后端两部分组成。

前端：开发者选择或构建 MoE 层。随后，性能分析模型会评估各 API 定义在不同输入规模下的执行时间，并使用机器学习算法（如线性回归）进行性能拟合，从而使调度器无需了解各子模块的具体实现细节。

后端：调度器利用为各模块建立的性能模型，自动优化任务工作流。后端在不涉及具体编程细节的前提下，以子模块为粒度识别并排列任务，而具体执行则由前端负责。

实现

我们基于 PyTorch 实现了 FSMoE，并使用其 C/C++ 与 CUDA 扩展机制。对于自定义算法，用户可以通过继承抽象接口来实现自己的 MoE 组件，如示例代码所示。

from FSMoE import ExpertBase, CallbackBase

class CustomizedExpert(ExpertBase):
    def do_experts(self, args):
        pass

class CustomizedCallBack(CallbackBase):
    def before_moe_start_hook(self, args):
        pass

from FSMoE import LinearGate, SimpleOrder, MOELayer

gate_impl = LinearGate()
order_impl = SimpleOrder()
moe_module = MOELayer(gate_impl, order_impl, **kwargs)

上述示例中，moe_module 可以作为 PyTorch 中的普通 nn.Module 实例使用。

任务的优化调度

受节点间与节点内通信重叠潜力的启发，我们在 MP 与 ESP 分组数量与单节点 GPU 数量一致的场景下，设计了一种新的调度方案，用于将所有耗时的通信任务（ESP-AllGather、ESP-ReduceScatter、AlltoAll Dispatch / Combine、Gradient-AllReduce）与计算任务（专家计算与注意力计算）进行流水化。

在该场景中，ESP-AllGather 与 ESP-ReduceScatter 属于节点内通信，而 AlltoAll Dispatch / Combine 与 Gradient-AllReduce 属于节点间通信。这一配置在实际中非常常见。就 MoE 框架而言，每一层包含的专家数量有限，但每个专家模型本身非常庞大，往往无法完全放入单个 GPU 中。例如，Mixtral-8x7B 与 Qwen1.5-MoE-A2.7B 在训练时都需要将单个专家划分到多个 GPU 上。

从硬件拓扑角度来看，节点间通信（通过 InfiniBand 或以太网）通常显著慢于节点内通信（如共享内存或 NVLink）。例如，NVIDIA H100 DGX 服务器配备了 8 张 200Gb/s 的网卡，节点间峰值带宽约为 100GB/s，而服务器内部的 NVLink 带宽可达 900GB/s，表明节点内带宽远高于节点间带宽。为了在精度与训练速度之间取得良好平衡，一种实用做法是将 MP 与 ESP 的规模对齐为单节点 GPU 数量。例如，在使用 8 张 A100-SXM4-80G GPU 的服务器上训练 Mixtral-8x7B，并设置 $N_{\text{MP}} = N_{\text{ESP}} = 8$ 时，该策略是完全可行的。此配置也可以通过模拟器进行仿真验证。

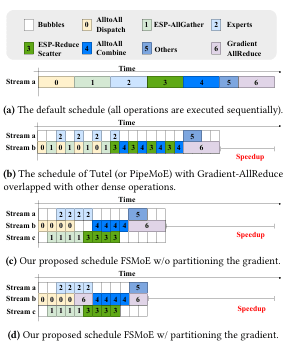fsmoe-3 图 3：在 $r = 4$ 的流水化深度下，DP+MP+EP+ESP 场景中四种反向传播调度方式：(a) 默认调度；(b) Tutel 改进版本（Tutel-Improved），使用 PipeMoE 将 Gradient-AllReduce 与其他稠密操作重叠；(c) 未进行梯度分区的 FSMoE 调度；(d) 本文提出的 FSMoE 调度。前向过程与反向过程类似，但不包含 Gradient-AllReduce。

如图 3d 所示，输入被划分为若干 chunks，并以流水线方式顺序处理。需要注意的是，Gradient-AllReduce 会紧随最后一个分块的 AlltoAll Dispatch 之后执行；同时，在反向阶段中，Gradient-AllReduce 也可以与 ESP-AllGather / ESP-ReduceScatter 以及专家计算进行重叠。前向阶段与反向阶段的流程基本一致，唯一的区别在于前向阶段不包含 Gradient-AllReduce。此外，最优流水线深度在不同阶段（前向与反向）之间并不相同，因此需要阶段特定的解决方案。

为了实现上述新的调度方案，我们首先像 PipeMoE 与 FasterMoE 一样，为不同耗时的计算与通信任务构建性能模型；随后基于这些性能模型构建一个优化问题，并提出一种高效的求解方法。

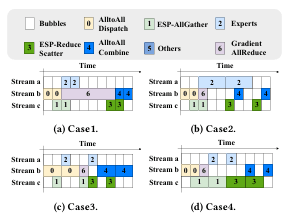fsmoe-4 图 4：在流水线深度 $r=2$ 时，对 ESP-AllGather / ESP-ReduceScatter、AlltoAll Dispatch / Combine、专家计算以及 Gradient-AllReduce 进行流水化调度的四种情况。(a) 情况 1：AlltoAll 通信慢于节点内通信与专家计算，但节点间通信（AlltoAll 与 Gradient-AllReduce）并不慢于节点内通信与专家计算。(b) 情况 2：专家计算不慢于节点间通信与节点内通信。(c) 情况 3：AlltoAll 通信不慢于节点内通信与专家计算。(d) 情况 4：节点内通信（AllGather 与 ReduceScatter）不慢于节点间通信与专家计算。

性能模型

当输入被划分为 $r$ 个分块时，AlltoAll、AllGather、ReduceScatter 以及专家计算在每个分块上的时间，分别记为 $t_{a2a,r}$、$t_{ag,r}$、$t_{rs,r}$ 和 $t_{exp,r}$。这些时间通过线性模型进行建模，其形式如下（将在第 6.2 节中验证）： $$ \begin{aligned} t_{a2a,r} &= \alpha_{a2a} + \frac{n_{a2a}}{r}\cdot \beta_{a2a},
t_{ag,r} &= \alpha_{ag} + \frac{n_{ag}}{r}\cdot \beta_{ag},
t_{rs,r} &= \alpha_{rs} + \frac{n_{rs}}{r}\cdot \beta_{rs},
t_{exp,r} &= \alpha_{exp} + \frac{n_{exp}}{r}\cdot \beta_{exp}. \end{aligned} \tag{1} $$ 其中，$n_$ 表示通信消息的大小或计算工作量，$\alpha_$ 表示启动开销，$\beta_*$ 表示每字节传输时间或每单位工作量处理时间。特别地，当每个专家计算包含多个相同的 通用矩阵乘（GEMM） 操作时，$\alpha_{exp}$ 与 $\beta_{exp}$ 可由 $\alpha_{gemm}$ 与 $\beta_{gemm}$ 乘以 GEMM 操作次数得到。

流水线深度的优化

计算与通信的性能模型为流水线深度 $r$ 的优化提供了基础。然而，直接对整体执行时间进行优化是困难的，因为其依赖于多种相互制约的因素。例如，ESP-ReduceScatter 的启动时间同时受到 ESP-AllGather（节点内通信竞争） 与 专家计算（数据依赖） 的约束。为降低问题复杂度，我们根据主要时间开销来源，将所有情况划分为图 4 所示的四类。在每一类中，通过聚焦于关键约束，可以更直接地获得最优解。

在讨论具体情形之前，先给出刻画这些情形的 七个约束条件：

  • Q1：$t_{a2a,r} > t_{ag,r}$ 若 Q1 为真，表示在分块输入上 AlltoAll 比 AllGather 更耗时；在假设 AllGather 与 ReduceScatter 耗时相近的情况下，AlltoAll 也会慢于 ReduceScatter。

  • Q2：$r \cdot t_{exp,r} > 2(r-1)\cdot t_{a2a,r}$ 若 Q2 为真，表示专家计算的耗时超过除首个 AlltoAll Dispatch 与最后一个 AlltoAll Combine 之外的通信时间。当 Q1 为真时，该结论同样适用于首尾分块的 AllGather 与 ReduceScatter。

  • Q3：$r \cdot t_{exp,r} > (r-1)\cdot t_{ag,r} + t_{rs,r}$ 若 Q3 为真，表示在 Q1 为假的情况下，专家计算的时间足以影响整体耗时。

  • Q4：$t_{gar} > t_{ag,r} + t_{rs,r}$ 若 Q4 为真，表示在 Q1 为真且 Q2 为假时，Gradient-AllReduce 的耗时足以影响整体时间。

  • Q5： $$ t_{gar} > r\cdot t_{exp,r} - 2(r-1)\cdot t_{a2a,r} + t_{ag,r} + t_{rs,r} $$ 若 Q5 为真，表示在 Q1 与 Q2 均为真时，Gradient-AllReduce 的耗时足以影响整体时间。

  • Q6： $$ t_{gar} > r\cdot t_{ag,r} + r\cdot t_{rs,r} - 2(r-1)\cdot t_{a2a,r} $$ 若 Q6 为真，表示在 Q1 为假且 Q3 为假时，Gradient-AllReduce 的耗时足以影响整体时间。

  • Q7： $$ t_{gar} > t_{ag,r} + t_{rs,r} + r\cdot t_{exp,r} - 2(r-1)\cdot t_{a2a,r} $$ 若 Q7 为真，表示在 Q1 为假且 Q3 为真时，Gradient-AllReduce 的耗时足以影响整体时间。

在此基础上，四种情形可表示如下。

情况 1

当 $(Q1 \wedge \lnot Q2 \wedge Q4)\ \vee\ (Q1 \wedge Q2 \wedge Q5)\ \vee\ (\lnot Q1 \wedge \lnot Q3 \wedge Q6)\ \vee\ (\lnot Q1 \wedge Q3 \wedge Q7)$ 成立时，表示 Gradient-AllReduce 足够大，使得 节点间通信（AlltoAll 与 Gradient-AllReduce） 主导了图 4a 中的整体时间开销。此时： $$ \begin{aligned} t^{moe}1 &= 2r \cdot t{a2a,r} + t_{gar}
&= 2r\alpha_{a2a} + 2n_{a2a}\beta_{a2a} + t_{gar}. \end{aligned} \tag{2} $$ 为获得最小值 $t_1^*$，需解如下问题： $$ \min f_1(r)=t^{moe}_1,\quad \text{s.t. } r\ge1. $$

情况 2

当 $(Q1 \wedge Q2 \wedge \lnot Q5)\ \vee\ (\lnot Q1 \wedge Q3 \wedge \lnot Q7)$ 成立时，Gradient-AllReduce 对整体时间影响很小，而专家计算在图 4b 中占主导地位。此时： $$ \begin{aligned} t^{moe}2 &= 2t{a2a,r} + t_{ag,r} + t_{rs,r} + r\cdot t_{exp,r}
&= 2\alpha_{a2a} + \frac{2n_{a2a}}{r}\beta_{a2a}

  • \alpha_{ag} + \frac{n_{ag}}{r}\beta_{ag}
  • \alpha_{rs} + \frac{n_{rs}}{r}\beta_{rs}
  • r\alpha_{exp} + n_{exp}\beta_{exp}. \end{aligned} $$ 对应的优化问题为： $$ \min f_2(r)=t^{moe}_2,\quad \text{s.t. } r\ge1. $$

情况 3

当 Q1 为真、Q2 为假且 Q4 为假 时，表示 Gradient-AllReduce 与专家计算主导整体时间，同时 AlltoAll 在分块张量上仍慢于 AllGather 与 ReduceScatter（见图 4c）。此时： $$ \begin{aligned} t^{moe}3 &= 2r\cdot t{a2a,r} + t_{ag,r} + t_{rs,r}
&= 2r\alpha_{a2a} + 2n_{a2a}\beta_{a2a}

  • \alpha_{ag} + \frac{n_{ag}}{r}\beta_{ag}
  • \alpha_{rs} + \frac{n_{rs}}{r}\beta_{rs}. \end{aligned} $$ 最小值 $t_3^*$ 通过求解： $$ \min f_3(r)=t^{moe}_3,\quad \text{s.t. } r\ge1 $$ 得到。

情况 4

当 Q1 为假、Q3 为假且 Q6 为假 时，表示 Gradient-AllReduce 与专家计算对整体时间影响很小，而 AllGather 与 ReduceScatter 在分块张量上慢于 AlltoAll，节点内通信在图 4d 中占主导地位。此时： $$ \begin{aligned} t^{moe}4 &= 2t{a2a,r} + r\cdot t_{ag,r} + r\cdot t_{rs,r}
&= 2\alpha_{a2a} + \frac{2n_{a2a}}{r}\beta_{a2a}

  • r\alpha_{ag} + n_{ag}\beta_{ag}
  • r\alpha_{rs} + n_{rs}\beta_{rs}. \end{aligned} $$ 对应的优化问题为： $$ \min f_4(r)=t^{moe}_4,\quad \text{s.t. } r\ge1. $$

算法

算法 1 使用 MoE 相关系数（$n_{a2a}, n_{ag}, n_{rs}, n_{exp}$）以及集群相关系数（$\alpha_{a2a}, \beta_{a2a}, \alpha_{ag}, \beta_{ag}, \alpha_{rs}, \beta_{rs}, \alpha_{exp}, \beta_{exp}$）来确定最优流水线深度。其中，$t_{gar}$ 为手动输入的值：在前向阶段将其设为 0，在反向阶段则由第 5 节的方法确定。FSMoE 支持在前向与反向两个阶段采用不同的流水线深度。该算法在训练开始前执行一次，并在估计完集群相关系数之后运行。solve 函数采用序贯最小二乘规划（SLSQP）求解器；在求解 $f_1,f_2,f_3,f_4$ 时具有二次收敛（算法 1 的第 1–4 行），其余操作的时间复杂度为 $O(1)$。

前向与反向的独立调度

由于反向传播中需要计算关于权重的梯度以及 DP 工作进程间的梯度同步，其任务与前向阶段不同，因此最优流水线深度也不同。为此，我们通过保存各计算操作的激活并显式计算梯度，手动实现反向传播。具体而言，反向阶段中的 $\alpha_{exp}, \beta_{exp}, n_{exp}$ 取值为前向阶段的 两倍，以容纳对权重与输入的导数计算。同时，前向阶段不进行梯度同步，因此令 $t_{gar}=0$；反向阶段中的 $t_{gar}$ 则由第 5 节所述算法确定。

反向传播的调度

由于 MoE 层中存在节点间通信，用于梯度同步的 Gradient-AllReduce 无法直接与 MoE 层完全重叠。为进一步隐藏 Gradient-AllReduce 的时间开销，需要进行专门的协同设计。我们提出一种自适应梯度分区方法，以最大化 Gradient-AllReduce 与其他操作之间的重叠。

该方法包含两个步骤： 步骤 1：计算所有层中可与 Gradient-AllReduce 重叠的部分（记为 overlappable parts）的时间开销；随后对梯度进行切分，并尽可能将其分配给这些可重叠部分。 步骤 2：对步骤 1 之后仍然剩余的梯度进行安排，并将分配到各个 MoE 层的剩余梯度作为变量进行优化。

性能模型

与第 4.1 节类似，AllReduce 的性能模型表示为 $$ t_{ar}(n_{ar})=\alpha_{ar}+n_{ar}\cdot\beta_{ar}, $$ 其中 $t_{ar}$ 为耗时，$n_{ar}$ 为通信消息大小，$\alpha_{ar}$ 为启动开销，$\beta_{ar}$ 为每字节传输时间。其逆函数表示为 $$ g^{inv}{grad}(t{ar})=\frac{t_{ar}-\alpha_{ar}}{\beta_{ar}}. $$

步骤 1：计算梯度分区

在该步骤中，我们首先令 $t_{gar}=0$，并使用算法 1为每个 MoE 层优化流水线深度，从而计算可重叠部分的时间开销。随后，尝试对梯度进行切分并分配给各层的可重叠部分，以最小化训练时间。依据上述性能模型，可以计算分配给每一层的梯度量。

为便于表述，我们将一个 MoE 层及其之后、直到下一个 MoE 层之前的其他操作统称为一个广义层。记第 $i$ 个广义层的梯度为 $n^{i}{grad}$，其可重叠部分的时间为 $t^{i}{olp}$。在该步骤中，分配给每一层的梯度数量表示为 $$ n^{i}{grad,first} = g^{inv}{grad}!\left(\min!\left(t_{grad}(n^{i-1}{grad}),, t^{i}{olp}\right)\right). \tag{3} $$ 若梯度未能完全重叠，则需按如下方式更新： $$ n^{i}{grad} = n^{i}{grad}

  • g^{inv}{grad}!\left(\max!\left(t{grad}(n^{i-1}{grad})-t^{i}{olp},,0\right)\right). \tag{4} $$

需要注意的是，可重叠时间 $t_{olp}$ 可拆分为稀疏 MoE 部分 $t_{olp,moe}$ 与稠密部分 $t_{olp,dense}$。其中，$t_{olp,dense}$ 可在训练前测量，而 $t_{olp,moe}$ 则在流水线深度优化过程中计算。具体地，当 $t_{gar}=0$ 时，会落入第 4.2 节中的 Case 2、Case 3 或 Case 4，此时 $$ t_{olp,moe}(r)= \begin{cases} r\cdot t_{exp,r}+t_{ag,r}+t_{rs,r}-2(r-1)t_{a2a,r}, & \text{Case 2},
t_{ag,r}+t_{rs,r}, & \text{Case 3},
r\cdot t_{ag,r}+r\cdot t_{rs,r}-2(r-1)t_{a2a,r}, & \text{Case 4}. \end{cases} $$ 完成上述过程后，若仍存在剩余梯度，则进入步骤 2。

步骤 2：优化分区

步骤 2 用于分配步骤 1 之后的剩余梯度。注意，不同的 Gradient-AllReduce 输入时间会使算法 1产生不同的流水线深度与时间开销，这表明剩余梯度仍可进一步分配到各个 MoE 层以最小化训练时间。

记第 $i$ 个广义层的剩余梯度为 $n^{i}{rem}$，将算法 1 记为 $f^{i}{moe}(t_{gar})$，其输入为 Gradient-AllReduce 的时间开销，输出为第 $i$ 个 MoE 层的时间开销。设分配给第 $i$ 个 MoE 层的剩余梯度为 $x^{i}{g}$，则优化模型表示为 $$ \begin{aligned} \min\ & f_g(X_g)=\sum{i=1}^{n_l} f^{i}{moe}!\left(t{grad}(x^{i}{g})\right),
\text{s.t. }& 0\le x^{i}{g}< n^{i}{rem}+\sum{j=i-1}(n^{j}{rem}-x^{j}{g}),\quad 0<i<n_l, \end{aligned} \tag{5} $$ 其中 $n_l$ 表示层数。由于该优化仅在训练前执行一次，因此无需过分关注求解时间；我们采用差分进化算法来求解该优化问题。

评估

实验设置

我们主要将 FSMoE 与 Tutel（及其优化版本 PipeMoE）进行比较，后者设计了一种自适应调度来确定流水线深度，重点在于在 DP+MP+EP+ESP 结构中对通信与计算进行流水化（如图 2 所示）。此外，我们还将 FSMoE 的端到端训练性能与 DeepSpeed-MoE 进行比较。我们的实现代码可在 https://github.com/xpan413/FSMoE 获取。

测试平台：实验在两个测试平台上进行。

  • Testbed-A：48-GPU 集群，由 6 个互联节点组成，每个节点配备 4 张 Nvidia A6000 GPU。
  • Testbed-B：32-GPU 集群，由 8 个互联节点组成，每个节点配备 4 张 Nvidia GeForce RTX 2080Ti GPU。 更详细的服务器配置见表 3。软件环境为 Ubuntu 20.04、CUDA 11.3、PyTorch 1.12、NCCL 2.12。

MoE 模型配置：我们选取表 4 所示范围内的输入参数组合，以覆盖多种典型的注意力层与 MoE 层配置。由于 2080Ti 的显存限制，在 Testbed-B 上 $L\in{256,512,1024}$。需要注意的是，我们选择 $N_{hscale}=H/M$ 的范围而非直接设置 $H$，这在真实应用中更为常见。$f=*$ 表示在门控时不丢弃令牌；ffn-type 表示 MoE 中专家的类型，其中 simple 表示传统的两层前馈稠密网络，Mixtral 表示使用 Mixtral 中的专家。此外，在 Testbed-B 中将 $N_{MP}=N_{ESP}=4$，使得 ESP-AllGather / ESP-ReduceScatter 为节点内通信，而 AlltoAll 与 Gradient-AllReduce 为节点间通信；在 Testbed-A 中相应地设置 $N_{MP}=N_{ESP}=8$。

项目 Testbed A Testbed B
CPU 双路 Intel Xeon Platinum 8358 @ 2.60GHz 双路 Intel Xeon Gold 6230 @ 2.10GHz
GPU 8× NVIDIA RTX A6000 @ 1.46GHz 4× NVIDIA RTX 2080 Ti @ 1.35GHz
显存 48 GB 11 GB
内存 512 GB DDR4 512 GB DDR4
GPU 互联 NVLink 112.5 GB/s（4 路） PCIe
PCIe 版本 PCIe 4.0 ×16 PCIe 3.0 ×16
网络 Mellanox MT28908 @ 200 Gb/s Mellanox MT27800 @ 100 Gb/s

表 3：测试平台中的服务器配置。

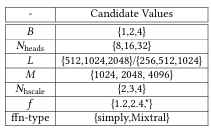fsmoe-5 表 4：注意力层与 MoE 层的配置。$N_{hscale}=H/M$；$f=*$ 表示门控阶段不丢弃令牌；ffn-type 表示 MoE 中专家的类型。

性能模型

我们需要获取与集群相关的输入参数，用于计算与通信的性能模型。我们通过微基准测试工具，在不同规模下测量 GEMM 计算以及 四种通信操作的耗时，并据此拟合式 (1) 中的性能模型。具体而言，我们使用 NCCL-2.12 的集合通信原语，并结合 nccl-tests 来评估不同消息规模下的通信耗时；同时，使用 PyTorch 中的 torch.matmul 函数，对不同形状矩阵的 GEMM 执行时间进行评估。

在通信建模中，选取 float 类型元素，规模范围为 $2^{18}$ 到 $24\times 2^{18}$，步长为 $2^{18}$，以模拟不同张量大小；在 GEMM 建模中，选取 float 类型元素，规模范围为 $2^{19}$ 到 $12\times 2^{19}$，步长为 $2^{19}$。每个测量结果均取 5 次运行的平均值 以保证一致性。结果如图 5 所示，可以看到，带截距项（即启动时间）的线性模型能够很好地拟合实际测量性能。

具体而言，我们的 GEMM 模型的 $r^2$ 为 0.9987；通信任务对应的 $r^2$ 分别为：

  • AllReduce：0.9999896
  • AlltoAll：0.9999
  • AllGather：0.9999653
  • ReduceScatter：0.9999599

在性能模型中，完成计算与通信参数测量的总耗时 小于 100 秒，采用最小二乘法进行拟合的时间 小于 10 毫秒。在完成拟合后，使用 SLSQP 求解流水线深度 $r$，在 1458 种配置下的平均耗时为 193 毫秒。当面对新的 GPU 集群时，仅需在模型训练前使用微基准测试 一次性估计参数，不会影响训练效率。

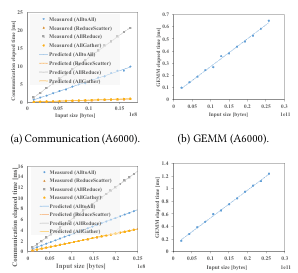
fsmoe-6

图 5：性能模型。标记点为实测值，曲线为基于估计参数的预测值。(a) Testbed-A 上的 GEMM：$\alpha_{gemm}=4.26\times10^{-2}$，$\beta_{gemm}=2.29\times10^{-11}$。(b) Testbed-A 上的通信：$\alpha_{a2a}=2.87\times10^{-1}$，$\beta_{a2a}=2.21\times10^{-7}$，$\alpha_{ag}=3.37\times10^{-1}$，$\beta_{ag}=2.32\times10^{-6}$，$\alpha_{rs}=3.95\times10^{-1}$，$\beta_{rs}=2.34\times10^{-7}$，$\alpha_{ar}=5.11\times10^{-1}$，$\beta_{ar}=4.95\times10^{-6}$。(c) Testbed-B 上的 GEMM：$\alpha_{gemm}=9.24\times10^{-2}$，$\beta_{gemm}=4.42\times10^{-11}$。(d) Testbed-B 上的通信：$\alpha_{a2a}=1.75\times10^{-1}$，$\beta_{a2a}=3.06\times10^{-7}$，$\alpha_{ag}=3.20\times10^{-2}$，$\beta_{ag}=1.68\times10^{-7}$，$\alpha_{rs}=3.91\times10^{-2}$，$\beta_{rs}=1.67\times10^{-7}$，$\alpha_{ar}=8.37\times10^{-2}$，$\beta_{ar}=5.99\times10^{-7}$。

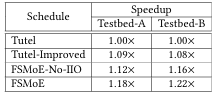fsmoe-7 表 5：在表 4 所示配置层上，四种调度方案相对于 Tutel（含其优化版本 PipeMoE）的平均加速比。Tutel-Improved 表示使用 PipeMoE 将 Gradient-AllReduce 与非 MoE 部分重叠；FSMoE-No-IIO 表示未进行节点间与节点内通信重叠的 FSMoE。

配置化层的性能

我们在图 2 所示结构下，对表 4 中给出的多种配置进行了实验，对比 FSMoE 与 PipeMoE。为验证梯度分区方法及其与 Gradient-AllReduce 的重叠调度，我们在配置层中显式加入了梯度聚合。为更全面的对比，还额外评估了两种调度方案：Tutel-Improved 与 FSMoE-No-IIO。其中，Tutel-Improved 表示使用 PipeMoE 将 Gradient-AllReduce 与非 MoE 部分重叠；FSMoE-No-IIO 表示 FSMoE 不进行节点间与节点内通信的重叠。

实验结果表明，仅将 Gradient-AllReduce 与非 MoE 部分进行简单重叠，便可相对于 Tutel（含 PipeMoE）获得 1.08×–1.09× 的加速；而结合自适应梯度分区以及节点间/节点内通信与计算的充分重叠后，FSMoE 在 1458 种配置上相对于 Tutel 实现了 1.18×–1.22× 的平均加速。通过对比 FSMoE 与 FSMoE-No-IIO 在表 5 中相对于 Tutel 的加速比，可以进一步看到，节点间与节点内通信的重叠能够显著提升性能。

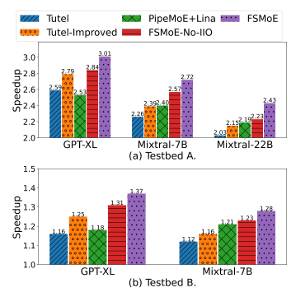fsmoe-8 图 6：FSMoE、FSMoE-No-IIO、Tutel、Tutel-Improved、PipeMoE+Lina（PipeMoE 结合 Lina 提出的固定块大小梯度分区调度）在 MoE 模型（GPT2-XL、Mixtral-7B、Mixtral-22B）上，相对于 DeepSpeed-MoE（DS-MoE）的加速比。

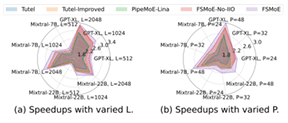fsmoe-9 图 7：在不同配置下，五种调度方案在 Testbed-A 上相对于 DS-MoE 的加速比。

MoE 模型上的性能

为评估端到端训练性能，我们在两个测试平台上，对 Mixtral-7B 与一个基于 GPT-2 的 MoE 模型进行了实验；此外，还在 Testbed-A 上评估了 Mixtral-22B。实验中设置 $B=1$、$k=2$、$f=1.2$。为实现节点间与节点内通信的重叠，设置 $N_{ESP}=N_{MP}$，在 Testbed-A 与 Testbed-B 上分别为 8 和 4。此外，专家数量 $N_{EP}$ 与节点数量相同，在 Testbed-A 与 Testbed-B 上分别为 6 和 8。序列长度 $L$ 在 Testbed-B 上设为 256，在 Testbed-A 上设为 1024。为保证模型能够在 Testbed-B（32×2080Ti，11GB）上运行，我们将 Mixtral-7B 的层数设为 7；受显存限制，Mixtral-22B 在 Testbed-A 上的层数设为 33。

为进一步分析，还引入了两种额外调度方案：Tutel-Improved（使用 PipeMoE 将 Gradient-AllReduce 与非 MoE 部分重叠）以及 PipeMoE+Lina（在反向传播中将梯度划分为固定大小块（如 30MB），并将梯度聚合与专家计算及非 MoE 部分重叠）。

图 6 的结果显示，相比 DeepSpeed-MoE，FSMoE 实现了 1.28×–3.01× 的加速，而 Tutel 仅能达到 1.16×–2.59×。此外，FSMoE 相对于 Tutel、Tutel-Improved、PipeMoE+Lina 和 FSMoE-No-IIO，平均分别获得 1.19×、1.12×、1.14×、1.07× 的加速，验证了自适应梯度分区方法与流水化调度的有效性。需要指出的是，Lina 采用固定块大小的梯度分区，难以适配多种配置，性能表现不稳定；而 FSMoE 能够自适应地分区梯度并调整流水线深度，从而获得更优结果。

启用流水线并行（PP）的 MoE 模型性能

我们还在 Testbed-A 上进一步启用了 流水线并行（PP）（$N_{PP}=2$，基于 GPipe 实现）。结果如图 8 所示，FSMoE 相对于 DS-MoE、Tutel、Tutel-Improved、PipeMoE+Lina 和 FSMoE-No-IIO，平均分别实现 2.46×、1.16×、1.10×、1.12×、1.05× 的加速。

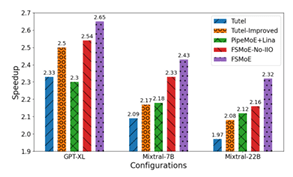fsmoe-10 图 8：在启用 PP 的情况下，五种调度方案在 Testbed-A 上相对于 DS-MoE 的加速比。

不同 $L$ 与 $P$ 下的性能

我们还在 Testbed-A 上分析了 FSMoE 在不同序列长度 $L\in{512,1024,2048}$ 与不同进程数 $P\in{16,32,48}$ 下的性能，结果如图 7 所示。当 $P=48$ 且 $L$ 变化时，FSMoE 相对于 DS-MoE 的平均加速分别为 2.17×、2.72×、3.14×，相对于 Tutel 的平均加速分别为 1.17×、1.19×、1.17×；当 $L=1024$ 且 $P$ 变化时，相对于 DS-MoE 的平均加速为 2.25×、2.27×、2.72×，相对于 Tutel 的平均加速为 1.20×、1.16×、1.19×。这些结果表明 FSMoE 具有良好的鲁棒性。

多种门控函数的支持

表 6 展示了在 Testbed-B 上，不同门控函数在真实世界 MoE 模型 GPT2-XL 上的时间性能。结果表明，在保持更高效率的同时，我们的框架能够良好地支持多种门控函数，体现了其可扩展性与灵活性。

fsmoe-11 表 6：Testbed-B 上，不同门控函数在真实世界 MoE 模型 GPT2-XL 中的时间性能（平均每次迭代耗时，单位：毫秒）。数值越小越好，括号中给出加速比。

相关工作

在优化 MoE 模型训练性能方面，已有研究主要从三个相互正交的方向展开，分别是 MoE 算法、AlltoAll 算法以及调度算法。其中，MoE 算法侧重于负载均衡与门控函数设计，AlltoAll 算法致力于提升数据分发与合并效率；而我们的工作主要关注 MoE 系统与调度算法，其目标是降低通信时间，因此本文主要介绍该方向上的相关研究。

Tutel 和 DeepSpeed-MoE 是用于训练 MoE 模型的代表性专用优化系统，二者集成了多种优化技术。然而，这些框架当前主要依赖于手动配置流水线深度或在受限搜索空间内的启发式搜索方法。与 Tutel 不同，FasterMoE 允许将输入令牌划分为两组，以实现专家计算与 AlltoAll 通信的重叠。在 Tutel 的基础上，PipeMoE 提出了一种创新且近似最优的输入令牌分区方法。Lina 则通过处理 AllReduce 与 AlltoAll 操作之间的挑战，旨在缓解反向传播阶段的网络竞争。

此外，还有一系列研究关注于通信与计算之间的细粒度重叠。T3 提出了一种软硬件协同设计方法，将串行通信与计算进行无缝融合，从而减少资源冲突。Wang 等人 通过使用语义等价的计算图变换来增强重叠能力，并在 XLA 中实现。Punniyamurthy 等人 研究了 DLRM 中的集合通信开销问题。FLUX 与 CoCoNet 将原本的通信与计算拆分为更小、更细粒度的单元，并将这些分块后的计算与通信融合为统一内核。Shi 等人 提出利用多通信流并发执行来提升 AllReduce 的带宽利用率。这些方法可从通信与计算资源竞争的角度进一步增强我们的方案。

结论

本文提出了一种名为 FSMoE 的灵活训练系统，用于优化 MoE 模型中的任务调度。为实现这一目标： 1）我们设计了 MoE 模块的统一抽象与在线性能分析，以支持多种 MoE 实现； 2）我们对节点内与节点间通信与计算任务进行协同调度，从而最小化通信开销； 3）我们提出了一种自适应梯度分区方法用于梯度聚合，并设计了能够自适应流水化通信与计算的调度策略。

在两个规模最高达 48 GPU 的集群上的实验结果表明，FSMoE 在 1458 种定制 MoE 层配置上，相比当前最先进的 MoE 训练系统（DeepSpeed-MoE 与 Tutel）实现了 1.18×–1.22× 的加速；在基于 GPT-2 与 Mixtral 的真实世界 MoE 模型上，实现了 1.19×–3.01× 的性能提升。

探索主题

阅读C++计算机架构k8s数据库分布式风格网络Go记录算法编译器编程范式统计操作系统MLAIRust设计